Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 5

                                        (7.8)

К эквивалентной линейной СУ можно применить известные критерии устойчивости. По критерию Найквиста, например, выполнение условия

                                                      (7.9)

соответствует состоянию СУ на границе устойчивости и наличию в ней незатухающих колебаний. Таким образом, возможность существования автоколебаний в системе проверяется путем решения уравнения (7.9), которое, с учетом (7.8), записывается в виде:

                                            (7.10)

и решается графически. Наличие точек пересечения годографов функций  и  означает, что уравнение (7.10) имеет решения при некоторых значениях частоты и амплитуды (существование автоколебаний возможно). Отсутствие точек пересечения годографов означает, что существование автоколебаний в рассматриваемой системе невозможно.

          Наличие решения уравнения (7.10) еще не означает, что режим автоколебаний устойчив и может существовать в системе неограниченно длительное время. Для проверки устойчивости режима автоколебаний необходимо исследовать поведение системы при изменении амплитуды автоколебаний. Пусть решению (7.10) соответствуют значения частоты ω₁ и амплитуды a₁, для которых выполняется условие  Дадим амплитуде автоколебаний положительное приращение a₁+Δa. В режиме устойчивых автоколебаний в системе должен действовать фактор стабилизации амплитуды: при случайном отклонении амплитуды от значения a₁ она должна восстанавливать свое значение. Это значит, что при увеличении амплитуды должно выполняться условие:  или 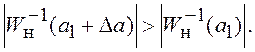 Таким образом, в режиме устойчивых автоколебаний положительное приращение амплитуды a₁+Δaдолжно соответствовать сдвигу точек на годографе  в направлении, указанном стрелкой и приводящему к удалению от начала координат.

          Удобно использовать следующее правило: режим автоколебаний в системе устойчив, если точка на годографе , соответствующая увеличению амплитуды, не охватывается годографом  (в смысле критерия Найквиста). В противном случае режим автоколебаний неустойчив.

          Задача определения амплитуды и частоты автоколебаний решается с помощью зависимостей  и , заданных в явном виде. Исходной величиной является значение модуля функций 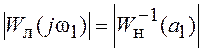.  Для определения частоты удобно использовать ЛХ.

          В качестве примера рассмотрим условия возникновения автоколебаний в двух СУ, содержащих реле с зоной нечувствительности (b=0,5; c=1) и линейные части с ПФ 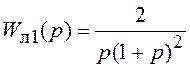 (первая система) и  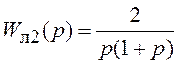(вторая система). Графическое решение уравнения (7.10) показано на рис. 7.8. Очевидно, что существование

автоколебаний возможно только в первой системе. Для этой системы уравнение (7.10) имеет два решения, соответствующие амплитудам автоколебаний a₁ и a₂. Согласно правилу проверки устойчивости режима автоколебаний, неограниченно длительное время в системе могут существовать лишь автоколебания с амплитудой a₁.

          Для определения амплитуды автоколебаний необходима зависимость  в явном виде (рис. 7.9, а). Точка пересечения годографов функций  и  соответствует значению   и, соответственно, . Функция  имеет две точки пересечения с единичным уровнем (рис. 7.9, а). Из рис. 7.8 следует: a₁>a₂, поэтому a₁≈1,15.

          Для определения частоты автоколебаний необходима зависимость  в явном виде. Для этого удобно использовать ЛХ (рис. 7.10, б). Поскольку точная ЛХ апериодического звена отличается на частоте сопряжения от асимптотической ЛХ на 3 дБ (см. разд. 1.4),

функция  равна единице на частоте ω₁=1, а частота автоколебаний равна ω₁/2π≈0,16 Гц.

7.5. Метод статистической линеаризации

Метод статистической линеаризации, предложенный отечественным ученым И.Е. Казаковым (1954 г.) и, практически одновременно, американским ученым  Р.К. Бутоном, позволяет определять вероятностные характеристики случайных процессов в СУ с существенно нелинейным элементом.

          Как и в методе гармонической линеаризации, рассматривается безынерционный НЭ, выходной сигнал которого y(t) проходит через узкополосную и, следовательно, инерционную линейную часть системы с ПФ W_л(p). Предполагается также, что статическая характеристика НЭ f(∙) симметрична и, кроме того, однозначна (дополнительное условие однозначности f(∙) введено с целью упрощения изложения метода статистической линеаризации). На вход НЭ поступает случайный процесс x(t) с нормальной плотностью вероятности (ПВ):