Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 7

          Для определения коэффициента K₁, в соответствии с (7.15), необходимо вычислить

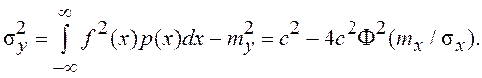
          Следовательно, коэффициент статистической линеаризации для

 центрированной случайной составляющей равен

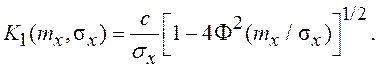                  (7.16)

          На рис. 7.12, а показана зависимость σ_y от m_x для нескольких значений σ_x, а на рис. 7.12, б – зависимость K₁(m_x,σ_x) (параметр с=1).

Замечание 1. Помимо критерия (7.13) известен и другой критерий, заключающийся в минимизации среднего квадрата разности процессов на выходах НЭ y(t) и заменяющего его линейного элемента y₁(t):

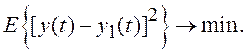                                  (7.17)

          Полагаем, что структура статистического эквивалента по-прежнему определяется уравнением (7.12). Тогда критерий (7.17) можно записать следующим образом:

  (7.18)

причем последнее слагаемое в левой части (7.18) удобно представить так:

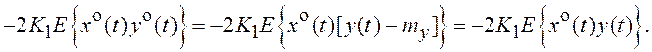
          Для определения коэффициентов статистической линеаризации K₀ и K₁ по критерию (7.17) следует приравнять нулю частные производные (7.18) по K₀ и K₁:

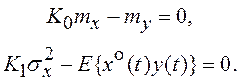
При этом

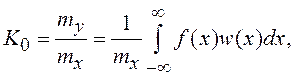                              (7.19)

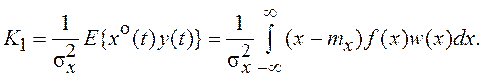              (7.20)

          Использование критерия (7.13) или (7.17) приводит к одному и тому же способу определения коэффициента статистической линеаризации для математического ожидания K₀ и разным способам определения коэффициента статистической линеаризации для центрированной случайной составляющей K₁. Выбор способа определения K₁ зависит от условий решаемой задачи и вычислительных затрат. Известна также рекомендация, в соответствии с которой следует в качестве K₁ использовать среднее арифметическое результатов вычислений с помощью (7.15) и (7.20). В некоторых случаях возможно использование упрощенных методов анализа нелинейной системы, инвариантных к способу определения K₁.

          Ранее, в качестве примера, был определен коэффициентK₁ для идеального реле по критерию (7.13). Приведем результат вычисления коэффициента K₁ для идеального реле по критерию (7.17):

                                 (7.21)

Замечание 2. Выше изложен метод статистической линеаризации, предложенный И.Е. Казаковым. Р.К. Бутон определил статистический эквивалент уравнением y₁(t)=Kx(t) с единственным коэффициентом K, общим для математического ожидания и центрированной случайной составляющей. В качестве критерия эквивалентности НЭ и заменяющего его линейного элемента использовалось условие (7.17), которое для одноканальной структуры статистического эквивалента можно представить так:

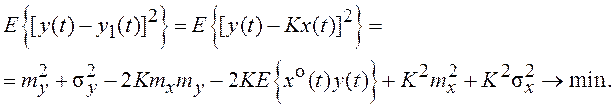      (7.22)

Для определения коэффициента K по критерию (7.22) следует приравнять нулю производную по K: 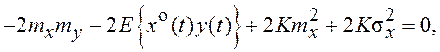  откуда

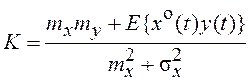  или, с учетом (7.19) и (7.20),

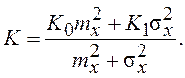
Коэффициент K представляет собой весовую сумму коэффициентов (7.19) и (7.20).

7.6. Применение метода статистической линеаризации для анализа нелинейных систем в стационарном режиме

          Рассматриваем замкнутую СУ, содержащую НЭ и линейную часть с ПФ W_л(p) (рис. 7.13). Полагаем, что все, рассмотренные в разд. 7.5, допущения выполняются (НЭ – безынерционный с симметричной однозначной статической характеристикой y=f(x), описывающей нелинейную дискриминационную характеристику; на вход НЭ поступает нормальный случайный процесс x(t), обусловленный шумом измерений v(t); линейная часть хорошо нормализует выходной случайный процесс НЭ y(t)). Полагаем также, что в нелинейной системе отсутствуют автоколебания.

          На вход нелинейной системы подается регулярное воздействие g(t) в аддитивной смеси с шумом v(t). Задана спектральная плотность мощности шума v(t):   (в рассматриваемой задаче дисперсия шума v(t) должна иметь конечное значение, поэтому аппроксимация v(t) белым шумом недопустима и следует задать зависимость).

          Случайные процессы x(t), y(t) и z(t) представляем в виде сумм математических ожиданий и центрированных случайных составляющих:

x(t)=m_x+ x^о(t),

y(t)=m_y+ y^о(t),

z(t)=m_z+ z^о(t).

          Нас интересует динамическая составляющая ошибки системы в стационарном режиме m_x=g-m_z, а также дисперсия флюктуационной составляющей ошибки