Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 4

          В качестве примера рассмотрим задачу определения эквивалентной ПФ реле с зоной нечувствительности (рис. 7.5). Статическая характеристика НЭ описывается выражением:

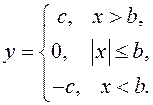
 В устройствах радиотехнического назначения наличие НЭ такого типа может быть обусловлено эффектами квантования сигнала. Статическая характеристика НЭ однозначная, поэтому  Согласно (7.4) и (7.5) имеем

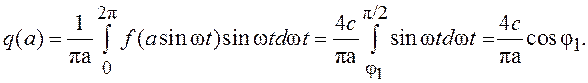
          Фазовый угол φ₁ и значение cosφ₁ легко найти из условия равенства (при ωt= φ₁) входного сигнала x(t)=a sinωt и зоны нечувствительности реле b: sin φ₁=b/a, откуда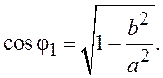

          Таким образом, эквивалентная ПФ реле с зоной нечувствительности равна

          Амплитуда первой гармоники выходного сигнала при  равна  а фазовый сдвиг первой гармоники относительно входного сигнала равен нулю (рис. 7.5). Заметим, что для идеального реле b=0 и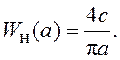  

          Рассмотрим более сложную задачу определения эквивалентной ПФ реле с гистерезисом (рис. 7.6 а). Статическая характеристика НЭ описывается выражением:

                              (7.7)

 В устройствах радиотехнического назначения могут использоваться не только электронные, но и электромеханические реле, для которых

характерна «петля гистерезиса» (срабатывание такого реле происходит с задержкой). Статическую характеристику вида (7.7) следует рассматривать не как функцию, а как безынерционную динамическую систему (рис. 7.6, б). Если система пребывает в состоянии y=-c, то при x<b   e=x-b<0 и система остается в прежнем состоянии, а при x>b   e=x-b>0 и система переходит в состояние y=c. Если система пребывает в состоянии y=c, то при x>-b   e=x+b>0 и система остается в прежнем состоянии, а при x<-b   e=x+b<0 и система переходит в состояние y=-c.

          Статическая характеристика НЭ неоднозначная, поэтому  Найдем эквивалентную ПФ НЭ, пользуясь полученными ранее результатами. Выходной сигнал НЭ представляет собой меандр с фазовым сдвигом φ₁=arcsinb/a. Амплитуда первой гармоники выходного сигнала такая же, как на выходе идеального реле:

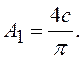 Представим входной и выходной сигналы в комплексной форме:  и 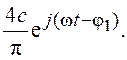 Их отношение определяет эквивалентную ПФ НЭ:

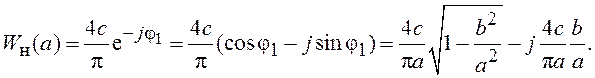
          Таким образом, вещественная часть эквивалентной ПФ реле с гистерезисом 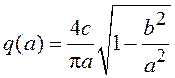 совпадает с W_н(a) реле с зоной нечувствительности, а коэффициент мнимой части 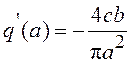 отличен от нуля.

          На рис. 7.7 показаны годографы функций  для реле с зоной нечувствительности (рис. 7.7, а), идеального реле (рис. 7.7, б) и реле с гистерезисом (рис. 7.7, в). Для реле с зоной нечувствительности точки годографа с ростом амплитуды a входного сигнала сначала приближаются к началу координат вдоль отрицательной части вещественной оси, а затем – удаляются, опять вдоль отрицательной части вещественной оси (рис. 7.7, а). Минимальное расстояние от начала координат имеет место при  и равно  Для идеального реле точки годографа с ростом амплитуды a входного сигнала перемещаются вдоль отрицательной части вещественной оси, удаляясь от начала координат (рис. 7.7, б). Для реле с гистерезисом годограф описывается комплексной функцией, причем коэффициент мнимой части не зависит от амплитуды входного сигнала a. Поэтому точки годографа с ростом амплитуды a входного сигнала перемещаются параллельно вещественной оси, удаляясь от мнимой оси (рис. 7.7, в). Удаление годографа от вещественной оси равно

7.4. Условия возникновения автоколебаний в нелинейной системе

          Рассматриваем замкнутую СУ, содержащую НЭ и линейную часть с ПФ W_л(p). Полагаем, что все, указанные в разд. 7.3, допущения выполняются (НЭ – безынерционный с симметричной статической характеристикой y=f(x); в системе, возможно, существуют автоколебания, причем линейная часть хорошо фильтрует все гармоники этого автоколебания, начиная со второй). Нас интересуют ответы на следующие вопросы:

- возможно ли существование автоколебаний в рассматриваемой системе?;

- если существование автоколебаний возможно, то устойчив ли режим автоколебаний?;

- если режим автоколебаний устойчив, то каковы амплитуда и частота автоколебаний?

          В соответствии с методом гармонической линеаризации заменяем НЭ линейным с эквивалентной ПФ ПФ W_н(a) и анализируем поведение эквивалентной линейной СУ с ПФ в разомкнутом состоянии