Физика макротел. Механика макроскопических тел, страница 5

 (12).

Разложение вектора ускорения по базису:

 

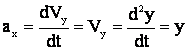
             M₁         V₁   A

                          

                   V₂ C      М₂

                    B

                                      V₂

V₁ и V₂ - скорости различные по величине и направлению.

 - геометрическое приращение скорости за время .

 На векторе V₂ отложим отрезок равный V₁.

V_к - характеризует изменение величины скорости за время  то есть .

V_п - характеризует изменение направления вектора скорости.

Согласно (11).

В пределе при  угол  при вершине треугольника (АМ₁С) стремится к нулю, а вектора V_к и V₂V₁, тогда  (13).

Тангенсальное или касательное ускорение характеризует быстроту изменения скорости по величине и всегда направлено по касательной в точке траектории.

а_т - тангенсальное ускорение.

Нормальное ускорение (равномерное движение точки по окружности).

Будем считать  бесконечно малым. Тогда точки М₁,М₂ и их скорости лежат в одной плоскости. Тогда бесконечно малая дуга представляет собой отрезок окружности с центром в точке О и радиусом ОМ₁=ОМ₂ М₁М₂=S .

  М₁

                     

    R                    М₂

 

       

0

 - радиус кривизны данной точки.

Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривизной на бесконечно малом участке.

Величина обратная радиусу кривизны называется кривизной траектории данной точки. Она характеризует скорость поворота касательной при перемещении вдоль кривой.