Физика макротел. Механика макроскопических тел, страница 10

                                                                V

                                          W                   

                                                  R

                                                             М

                                                0

 (1).

 (2).

 (3) - модуль линейной скорости точки М.

 (4) - Модуль угловой скорости точки.

 - Векторная величина, равная отношению элементарного поворота тела к длительности поворота или величина, характеризующая быстроту изменения угла поворота.

W - Направлена по оси вращения и связаны с направлением вращения, правилом правого винта.

В международной системе СИ угол поворота равен .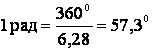

Согласно 2:

V=RW (5) – формула связывает модули линейной и угловой скорости.

Вращательное движение называется равномерным движением, если модуль угловой скорости в процессе вращения постоянен. В этом случае угол поворота прямопропорционален времени вращения.

 (6).

Равномерное движение можно охарактеризовать величиной, которую называют периодом вращения – это время, за которое тело совершает один полный оборот, то есть поворачивается на угол.

                           .

                       

                       

V - частота вращения – число оборотов в единицу времени.

 (9).

 (10).

Понятия Т и V можно сохранить и для неравномерного движения.

При этом под мгновенным значением t понимают время, за которое тело бы совершило один оборот, с данным значением угловой скорости.

  V - такое число оборотов, которое совершило бы тело за единицу времени при аналогичных условиях.

Условия ускорения.

Согласно формуле V=RW.

 (11)

 (12)

(13) - абсолютное значение линейного касательного ускорения.

(14) - абсолютное значение угловой скорости.

 (14^/)  

Угловое ускорение характеризует быстроту изменения угловой скорости.

Согласно 12 можно записать:

a_к=R (15).

Равенства: , V=RW, a_к=R показывают, что линейные величины характеризующие вращения отдельной точки получают из соответствующих угловых величин, характеризующих вращение всего тела, путем умножения на радиус вращения.

Если тело вращается вокруг неподвижной оси ускоренно, то есть , то вектор углового ускорения направлен по оси вращения  и совпадает по направлению с угловой скоростью вращения.