Физика макротел. Механика макроскопических тел, страница 3

IV. Вектором перемещения точки за промежуток времени от до  называется приращение радиус – вектора

Точки за рассматриваемый промежуток времени.

Перемещение характеризует изменение положение точки в пространстве за время .

 (5).

Вектор перемещения направлен вдоль хорды, оттягивающей соответствующий участок траектории из положения точки  в момент времени t₁, в ее положение в момент времени t₂.

Во всех случаях, кроме прямолинейного абсолютная величина вектора перемещения меньше пути, то есть.

Для прямолинейного движения .

Для криволинейного движения  - выполняется в пределе для бесконечно малого промежутка времени, то есть при .

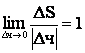 (6).

Вектор перемещения можно представить согласно формуле 1 в виде геометрической суммы перемещения.

V.Скорость характеризует:

1.  Быстроту изменения движения.

2.  Направление движения.

Для случая неравномерного движения используют два понятия:

1.) Средняя скорость – это вектор V_ср равный приращению радиус – вектора за промежуток времени от t₁ до  к длительности этого промежутка, то есть

 (7).

Вектор V_ср направлен вдоль хорды, стягивающей соответствующую часть траектории.

;

Исходя из этого, для прямолинейного неравномерного движения используют понятия средней путевой скорости:

 - все величины скалярные (8).

Переходя к пределу для бесконечно малого промежутка времени, то есть , из выражения (7) получают вектор истинной или мгновенной скорости – это скорость в данный момент времени или в данной точке траектории.

 (9).

Скорость в данный момент времени есть вектор равный первой производной по времени радиус – вектора этой точки.

Согласно 9 =>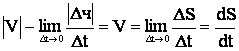

Скорость численного характеризует расстояние, которое проходит точка (в случае равномерного движения) или прошла бы (при неравномерном движении) за 1 секунду.

dt - дифференциал аргумента.

 - произвольное (конечное) приращение аргумента.

dt - Малое(элементарное) приращение аргумента.

Поскольку скорость – это вектор, то ее можно разложить по базису.