z

![]()
![]()
![]()
![]()
ez ч
![]()
![]()
![]()

![]() x
x ![]() ex 0 ey
ex 0 ey ![]() y
y
1.x, y, z – координаты радиус – вектора относительно базиса.
2. ![]() (1).
(1).
величины x, y, z – равны проекциям радиус-вектора на координатную ось.
![]()
![]() (2)
(2)
![]()
![]()
Для любой системы отчета радиус – вектор, а => положение точки в пространстве определяется тремя числовыми величинами, каждая из которых может меняться независимо друг от друга, поэтому говорят, что материальная точка обладает тремя степенями свободы.
II. С течением времени координаты точки в пространстве меняются.
Х=х(t)
Y=y(t) (4)
Z=z(t)
Ч=ч(t) (3)
Совокупность последовательных положений точки при ее движении образуют линию, которую называют траекторией движения точки.
Траектория – это кривая, которая описывает в пространстве конец радиус – вектора.
Различают прямолинейное и криволинейное движения. По характеру, движение делится на равномерное и неравномерное.
Траектория
описывается некоторыми понятиями: центр и радиус кривизны, а также вектор
главной нормали n - это единичный вектор, который направлен от точки М
траектории к центру кривизны, единичный вектор касательной ч, который направлен
по касательной к т. М траектории по направлению движения ![]() .
.
III. Длиной пути называется расстояние S, пройденная точкой за рассматриваемый промежуток времени и измеренное вдоль траектории по направлению движения.
Длина пути ровна сумме длин всех участков траектории, по которой движется точка за рассматриваемый промежуток времени, поэтому длина всегда положительна.
А
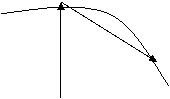 |
Ч1(t1) ![]()
![]() В
В
![]()
0
t1, А: ОА=ч1(t1)
![]()
В: ОВ=ч2(t2)
От t1 до ![]()
AB=![]() за
за
![]()
![]() есть длина траектории, которую описывает точка за
промежуток времени
есть длина траектории, которую описывает точка за
промежуток времени ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.