Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 9

(4)

0,05

0,22

0,08

001       а₂         0,15

011       а₃         0,12      1

(2)

010       а₄         0,1       0                       

0,13

00011   а₅         0,04      1

(3)

00010   а₆         0,04      0

(1)

00001   а₇         0,03      1

00000   а₈         0,02      0

1.  Находят 2 буквы с вероятностями (а₇ и а₈) и проводят от них линию к точке, в которой вероятность равна их сумме

2.  Теперь меньшими вероятностями обладают буквы а₅ и а₆. Соединяют их линиями в одной точке с вероятностью 0.08

3.  Соединяем 0,08 и 0,05, получает 0,13

4.  Соединяем буквы а₃ и а₄

5.  Соединяем 0,15 и 0,13

И так далее…

Кодируем ветки

Обозначим цифрой один верхнюю линию узла, нижнюю ноль.

Коды представляют собой последовательность 0 и 1, которые встречаются по пути от точки с вероятностью единица, до кодируемой буквы.

Передача информации по дискретным  каналам связи

Для анализа информационных возможностей канала связи используется обобщённая информационная модель каналов связи.

 

                    Z                    X                                 Y                     И

							ПИ

П2

П1

ИИ

                  ЛС

ИИ – источник информации

П₁, П₂ – преобразователи

ЛС – линия связи

ИП – источник помех

ПИ – приёмник информации

Источник информации создаёт cигналы z, которые кодируются в преобразователе П1, превращаются в сигналы x и поступают в линию связи (ЛС). В результате действия помех, сигнал Y на приёмном конце, отличается от X. Помехи создаются воображаемым источником помех (ИП) и поступают в линии связи в виде мешающего сигнала. Преобразователь П2 декодирует сигналы, и передаёт в приёмник информации. Приёмник информации перерабатывает принятое сообщение. Для организации эффективной передачи информации решают три задачи:

1.  Определение максимально  возможной скорости передачи информации по каналу;

2.  Разработка кодов, позволяющих увеличить скорость передачи информации;

3.  Согласование канала с источником.

Важнейшей характеристикой канала является пропускная способность (обозначается символом С). - Наибольшая возможная скорость передачи информации по каналу. Пропускная способность определяют следующим образом:

, где V_x- средняя скорость передачи символов, I_y®x – максимальное возможное значение среднего количества информации на один символ принятого сигнала.

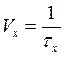   ,    - средняя длительность передаваемых символов

Взаимная информация

                - характеризует потери информации.

При отсутствии помех H(x / y) = 0 и . А максимальные I_y®x = log₂m

Пропускная способность канала

            m – количество символов алфавита, который кодируется

Основная теорема Шеннона о кодировании

для дискретного канала без помех

1). Дискретный канал без помех:

Основная теорема Шеннона утверждает: если источник информации имеет энтропию H(z), а канал связи обладает пропускной способностью, то:

 1. Сообщения, вырабатываемое источником всегда можно закодировать так, чтобы скорость их передачи  v_z была сколь угодно близка к v_{z max} .

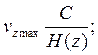
 2. Не существует способа кодирования, позволяющего сделать эту скорость больше, чем v_{z max.}

Величина  - называется потоком информации, т.е. согласно Шеннона, при потоке информации   существует способ кодирования,  при котором можно вырабатывать всю информацию, переданную источником. Если  то такого способа кодирования не существует.