Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 2

Система имеющая пять состояний

бит/символ   xi	x1	x2	x3	x4	x5
p1	0.01	0.01	0.01	0.01	0.96

Иногда энтропию определяют через математическое ожидание

H(x) = M[-log₂ p(x)] – это позволяет упростить математические выкладки.

Пример: Алфавит состоит из букв a, b, c, d. Даны вероятности p_a = p_b = 0,25; р_с = 0,34; p_d = 0.16

H(x) = - (2*0.25 log 0.25 + 0.34 log 0.34 + 0.16 log 0.16) = 1.952 бит/символ

Энтропия сложной системы

Под объединением двух систем X и Y с возможными состояниями x₁,x₂,…,x_n , y_1, y_2,…,y_{m ,} понимается сложная система (x, y), состояние которых x_i,y_i; представляют собой все возможные комбинации состояний x_i,y_i .

Число возможных состояний равно m х n.

Обозначим символом p_i,j , вероятность того, что система может находиться в состоянии p(x_i,y_i). Тогда вероятность p_ij можно представить в виде таблицы совместных вероятностей.

таблица совместных вероятностей   xi & yi	x1	x2	…	xn
y1	p11	p21	…	pn1
y2	p12	p22		pn2
…	…	…	…	…
ym	p1m	p2m	…	pnm

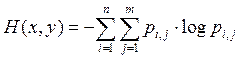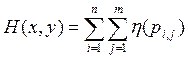;           ;         H(x, y) = M[- log p(x, y)].

Пусть системы X, Y независимы. Тогда по теореме умножения вероятностей имеем:

p(x, y) = p(x) * p(y)

Прологарифмируем левую и правую часть

log p(x, y) = log p(x) + log p(y)

H(x, y) = M[- log p(x) – log p(y)]

H(x, y) = H(x) + H(y), если независимые системы, то их энтропии складываются.

Условная энтропия. Объединение зависимых систем.

Пусть имеем две зависимые системы X и Y. Пусть система X приняла состояние x_i, а система Y приняла состояние y_i , тогда обозначим p(y_{i /} x_i) – это условная вероятность того, что система Y примет состояние y_i, при условии, что система X приняла состояние x_i.

Неопределённость системы в состоянии Y определяется частной условной энтропией.

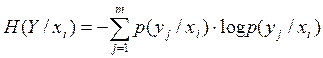 - система X находится в конкретном состоянии

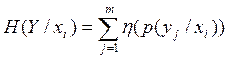;               - условное математическое ожидание

Полная условная энтропия

Для определения полной условной энтропии, каждая частная условная энтропия умножается на вероятность соответствующего состояния и все произведения складываются.

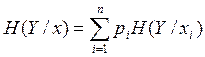  p_i = p(x_i) – вероятность наступления события x_i

;           

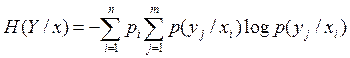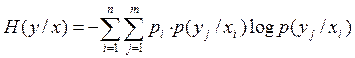
p_i * p(y_j / x_i) = p_ij

Тогда

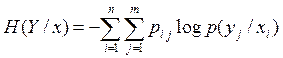;              H(Y / x) = M[ - log P(y / x)]

В целом полная условная энтропия характеризует степень неопределённости состояния системы Y, оставшуюся после того, как состояние системы X полностью определилось.

Пример: Имеются две системы, объединённые в одну, вероятности состояния которых заданы таблицей совместных вероятностей. Определить полную условную энтропию.

	Определим вероятности каждого события. Для этого складываем pij по столбцам.

 

xi & yi	x1	x2	x3	rj
y1	0.1	0.2	0	0.3
y2	0	0.3	0	0.3
y3	0	0.2	0.2	0.4
pi	0.1	0.7	0.2

Построить таблицу условных вероятностей p(y / x).      в каждой строке

yi& xj	x1	x2	x3
y1	1	0.2/0.7	0
y2	0	0.3/0.7	0
y3	0	0.2/0.7	1

 бит/символ

Составим таблицу условных вероятностей P(x / y).     

xi& yi	x1	x2	x3
y1	0.1/0.3	0.2/0.3	0
y2	0	1	0
y3	0	0.2/0.4	0.2/0.4