Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 18

= F(x) – это цикловой код.

Т.о. получается два способа образования циклического кода:

1) Путём умножения одной из комбинаций информационной части кода на образующий многочлен:

Q(x) * K(x) = I(x)

2) Умножение заданной комбинации на одночлен и той же степени, что и выбранный образующий многочлен с добалением остатка от деления.

Эти способы являются теоретическим основанием для построения кодирующих и декодирующих устройств.

Образующий многочлен K(x) принимает участие в образовании в каждой кодовой комбинации. Поэтому любой многочлен циклического кода делится на образующий без остатка. Если при делении обнаружен остаток, значит принятая комбинация содержит ошибку.

Для построении циклических кодов обычно используют образующую матрицу.

Способы построения образующей матрицы:

Первый способ

1) Образующая матрица получатся как результат слияния двух матриц: Первая - единичная повёрнутая размером n_u.

n_u = 4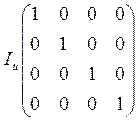                                  

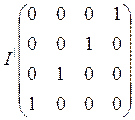
Дополнительная матрица имеет n_u – строк и n_k – столбцов. Для определения строк дополнительной матрицы используют результаты делений последней строки первой повёрнутой матрицы на образующий многочлен.

1 0000 … k(x)

 

В качестве строк дополнительной матрицы используются остатки от деления.

Пример: k(x) = 1011

Рассмотрим процедуру деления

Остаток 011 110 111 101 001 010 100

100000…  1011

1011

  01100

    1011

      1110

      1011

         1010

         1011

           001000

               1011

 

В дополнительной матрице используются лишь те остатки, вес которых W = d₀ – 1.  d₀ – минимальное кодовое расстояние. Строки образующей матрицы представляют собой первые комбинации искомого кода. Остальные комбинации получают суммированием различных сочетаниям строк.

Второй способ

Образующая матрица может быть построена в результате умножения элементов единичной матрицы размером n_u на образующий многочлен.

Третий способ

Образующая матрица может быть получена в результате циклического сдвига любой комбинации, полученной по способу два.

Декодирование циклических кодов

Остатки от деления полученного вектора на образующий многочлен является опознавательным. Идея обнаружения ошибки заключается в следующем принятая кодовая комбинация делится на образующий многочлен. Если есть остаток, то производится циклический сдвиг принятой кодовой комбинации. Затем сдвинутая комбинация снова делится на образующий многочлен. После ряда циклических сдвигов определяется такое положение, при котором остаток минимален.

Таблица неприводимых двоичных многочленов

Код	Многочлен	Код	Многочлен
11	x + 1	10001	x4 + 1
101	x2 + 1	10011	x4 + x + 1
111	x2 + x +1	10101	x4 + x2 +1
1001	x3 + 1	10111	x4 + x2 +x + 1
1011	x3 + x +1	11001	x4 + x3 + 1
1101	x3 + x2 + 1	11011	x4 + x3 + x + 1
1111	x3 + x2 + x + 1	11101	x4 + x3 + x3 +1
		11111	x4 + x3 + x2 + x + 1

Построение декодированного конкретного циклического кода

Код, исправляющий одиночную ошибку. d₀ = 3.

1) Расчёт соотношении между контрольными и информационными символами кода.

n_k = log((n_u + 1) + log(n_u + 1))

2) Выбор образующего многочлена производится по таблице непреводимых двоичных многочленов. Образующий многочлен следует выбирать с минимальным числом элементов. Его степень должна быть больше или равна числу контрольных разрядов. Число элементов должно быть .

Пример: Построим циклический код d₀ = 3 для передачи шестнадцати сообщений.

n_u = 4               n_k = 3

k(x) = 1011                   Строим единичную повёрнутую матрицу размером n_u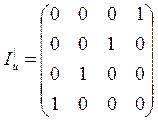           

Находим остатки от делений последовательной строкина образующий многочлен.