При наличии одной ошибки проверкой на чётность можно обнаружить ошибку. Проверки по позициям укажут номер ошибочной позиции. При наличии двойной ошибки, проверка на чётность не фиксирует ошибку. Проверки по позициям укажут наличие ошибки.
Пример: Построить код Хэминга для исправления одиночной и обнаружения двойной ошибки четырёх значного двоичного кода.
0001 nu = 4 nk = 3
Макет кода
а1а2а3а4а5а6а7
k1k20k3001k4
Схема проверок:
1) a1 + a3 + a5 + a7 = k1 + 0 + 0 + 1 = 0 Þ k1 = 1
2) a2 + a3 + a6 + a7 = k2 + 0 + 0 + 1 = 0 Þ k2 = 1
3) a1 + a5 + a6 + a7 = k3 + 0 + 0 + 1 = 0 Þ k3 = 1
|
1101001k4 Количество единиц чётное, следовательно сам код
Рассмотрим пример для vk = 01001011. Пример обнаружения единичной ошибки.
|
vk = 01001011 Þ ошибка в четвёртом разряде
vx = 01011011
1) Проведим проверки на чётность, которые указывают наличие одиночной ошибки.
2) Проведим проверку по позициям.
Составляем схему проверок
1) a1 + a3 + a5 + a7 = 0 + 0 + 1 + 1 = 0 Þ s1 = 0
2) a2 + a3 + a6 + a7 = 1 + 0 + 0 + 1 = 0 Þ s2 = 0 Þ S = (001) ® a4
3) a1 + a5 + a6 + a7 = 1 + 1 + 0 + 1 = 1 Þ s4 = 1
Пример: Обнаружение двойной ошибки.
Vk = 01001011
Vx = 11011011
1) Делаем проверку на чётность, число единиц чётное, следовательно, проверка ошибки не обнаруживает.
2) Делаем проверки по позициям
Схема
1) a1 + a3 + a5 + a7 = 1 + 0 + 1 + 1 = 1 Þ s1 = 1
2) a2 + a3 + a6 + a7 = 1 + 0 + 0 + 1 = 0 Þ s2 = 0 Þ S = (101)
3) a1 + a5 + a6 + a7 = 1 + 1 + 0 + 1 = 1 Þ s3 = 1
В этом случае S не указывает разряд ошибки, но S просто показывает, что она есть.
Циклические коды
Циклические коды названы так, потому что у них часть комбинаций может быть получена путём сдвига одной или нескольких комбинаций. Для проверки и обнаружения ошибок используется операции циклического сдвига. Циклические коды относятся к числу систематических кодов.
Идея построения циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов.
Не приводимыми называют многочлены, которые делятся без остатка на себя и на единицу. Под полем двоичных чисел подразумевается, что все операции проводятся по правилам сложения (и т.д.) двоичных чисел. Неприводимые многочлены играют роль производящих многочленов. Если информацию кодовой комбинации умножить на выбранный неприводимый многочлен, то получим циклический код. Корректирующая способность кода будет определяться видом неприводимого многочлена. В теории циклических кодов, кодовые векторы принято представлять в виде полиномов.
x3x2x1x0
Например: u(x) = x3 + x2 +1 ® 1 1 0 1
Построим циклический код. Образующий многочлен к(х) = х3 + х + 1 = 1011. При построении циклических кодов существует несколько приёмов.
1. Умножим кодовый вектор u(x) на одночлен той же степени, что и образующий многочлен.
u(x) * xn = (x3
+ x2 + 1) * x3 = x6 + x5 + x3
= 1101000
инф.. корректирующие разряды
часть
Чтобы уточнить значения корректирующих
разрядов производят деление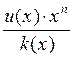 
. Делить можно используя
полиномы и значения двоичных разрядов.
Разделим один многочлен на другой
1101
000 1011 ® 001
1011
1101001
1100
1011
1110
1011
1010
1011
001 ® остаток от деления - он прибавляется к исходной
комбинации
1101000
+ 001
1101001 - искомый циклический код
В общем виде можно записать
, где
Q(x)
– частное; K(x)
– остаток
Умножим левую и правую часть k(x) и получим:
u(x) * xn = Q(x) * K(x) + R(x)
u(x) * xn + R(x) = Q(x) * K(x) – знак перед R(x) не имеет значение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.