Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 13

Пример: Определить количество информационных разрядов кода длиной в пятнадцать символов, если код исправляет две ошибки.

n=15

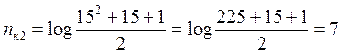
n_и  = n - n_к = 15 – 7 = 8

Исправление ошибок с помощью полной

кодовой таблицы

Процесс исправления ошибок поясняется с помощью диаграммы.

A_k – разрешённые комбинации                                    B_j – запрещённые комбинации

А₁ может искажена и может превратиться в B₁ или B₂ и т.д. в любую из запрещённых комбинаций. Запрещённые комбинации делятся на подмножества H_k.

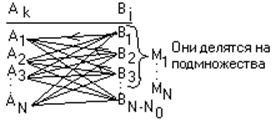Способ приема состоит в том, что если принимается комбинация B_j, которая попадает в подмножество М_к, то считается, что принята комбинация А_к (M₁ соответствует тому, что передавалась комбинация A₁).

Исправляющая способность кода будет зависеть от выбора разбиения или от стратегии.

Пример: Рассмотрим пример построения КУ. Пусть l_i – вектор ошибки, он имеет те же размерность, что и кодовая комбинация. 1 – искажения есть, 0 - искажений нет. Пусть кодируется набор из 4-х комбинаций.

А₁=0001

А₂=0101

А₃=1110

А₄=1111

Bj=А_к+l_i

li	Ак				q
	0001	0101	1110	1111	1
0001 0010 0100 1000	0000 0011 - 1001	0100 0111 - 1101	- 1100 1010 0110	- 1101 1011 0111
0011 0101 1001 0110 1010 1100	0010 0100 1000 0111 1011 1101	0110 0000 1100 0011 - 1001	1101 1011 0111 1000 0100 0011	1100 1010 0110 1001 - 0011	2
0111 1011 1101 1110	0110 1010 1100 -	0010 - 1000 1011	1001 - 0011 0000	1000 0100 0010 -	3
1111	-	1010	-	0000	4

Разбиение

Разбиение запрещенных кодовых комбинаций на множества зависит от статистики ошибок и выбранной стратегии. Если ошибки в каждом символе независимы, то вероятность ошибок убывает с повышением ее кратности. Для уменьшения средней вероятности ошибки следует в начале исправлять ошибки меньшей кратности.

На практике действуют следующим образом: оставляют комбинации в сроках с низшей кратностью и вычеркивают одинаковые комбинации в строках с высшей кратностью. Действуя, таким образом получают таблицу комбинаций:

М1	М2	М3	М4	q
0000 0011 1001	0100 0111 -	1100 1010 0110	1101 1011 -	1
0010	-	1000	-	2

Т.е. Исправили десять одинарных и две двойные ошибки.

Если статистика ошибок такова, что большую вероятность имеют ошибки высшей кратности, то разбиение изменяют: оставляют комбинации в строках с высшей кратностью и вычеркивают в строках с низшей.

 “-“ значит действие помехи переходит в разрешенную комбинацию и мы ее обнаруживаем.

М1	М2	М3	М4	q
1101	-	0111	-	2
0110 1100	1000 1011	0001 0011	0100 0010	3
-	1010	-	0000	4

Если статистика ошибок такова, что какая-нибудь комбинация искажается больше, чем другие, например, комбинация А₁, то стратегия разбиения будет другая: оставляем все кодовые комбинации соответствующие А₁, т.е.  М₁, а остальные вычеркиваем: комбинации, которые не совпадают, остаются

А1 М1	А2 М2	А3 М3	А4 М4	q
0000 0011 1001	- - -	1100 0010 0110		1
0010 0100 1000 0111 1011 1101				2

Систематические коды

Это коды, в которых контрольные и информационные разряды размещаются по определенной системе. Закономерности, заложенные в структуре этих кодов, позволяют проводить декодирование более простым способом, чем методом полной кодовой таблийы.