Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 12

А₃ = 10          0 Å 1 = 1             нечетн. – 1

А₄ = 11          1 Å 1 = 0

Определим кодовую комбинацию

А₁ÅА₂       Å            d = 1                  А₃ÅА₄       Å          d = 1

                                   01                                                              01

Для кода 2  

А₁=000      А₂ÅА₄     011                         А₃ÅА₂         101

А₂=011                     110    d = 2                                 011    d = 2

А₃=101                     101                                             110 

А₄=110

Ошибку можно не только обнаружить, но и исправить, если принятая кодовая комбинация ближе к исходной, чем к любой другой разрешённой комбинации.

Пример: Построим код: К коду 2 добавим два символа, повторив первых два символа получим код 3:

Код 2  

А₁=000

А₂=011

А₃=101

А₄=110

            Код 3

00 01 10 11

000 101 110 011

         информационные разряды         контрольные разряды

Определим кодовое расстояние между комбинациями

Строим матрицу кодовых расстояний

Пусть передаётся комбинация А₃, и она содержит ошибку

                                                                матрица кодовых расстояний

	А1	А2	А3	А4
Vx	4	3	1	2

v_x ближе всего к А₃, следовательно посылалась А₃ и мы ошибку исправили.

Корректирующая способность кода зависит от минимального кодового расстояния d₀. Если

d₀ = 3, то он может исправлять ошибку, то есть корректирующую способность кода можно повышать, если увеличивать минимальное кодовое расстояние.

Для построения кодов, которые обнаруживают и исправляют одиночную ошибку d₀ = 3, должно выполняться неравенство:

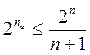,  где

n_и – количество информационных разрядов

n – значность кода

n_к – количество контрольных разрядов

n = n_и + n_к

Поэтому результаты сведем в таблицу:

n	5	6	7	8	9	10	11	12	13	14	15
nи	2	3	4	4	5	6	7	8	9	10	11
nк	3	3	3	4	4	4	4	4	4	4	4

Предположим, что строим код на тридцать два сообщения n_и = 5, выделяем столбец

n_к = 4

n = 9

Расчеты можно вести по формуле.

Для кода, который обнаруживает двойную ошибку, а исправляет одиночную:

- значения округляются в большую сторону

 - до большего целого числа

Обозначим буквой:

r – кратность обнаруживающих ошибок;

s – кратность исправляемых ошибок;

Тогда для кодов обнаруживающих и исправляющих ошибки:

d₀ = r + s + 1,

для кодов, которые только обнаруживают ошибки d₀ = n + 1,

для кодов, которые только исправляют ошибки d₀ = 2s + 1 (когда r > s).

Если

d₀   r    s

1    0   0                 отличие комбинации 

2    1   0                             обнаружение одиночной ошибки

3    1   1                 обнаружение одиночной ошибки и исправление одиночной ошибки

3    2   0                обнаруживающий 2-ую ошибку

Количество контрольных разрядов и значность кода для разных минимальных кодовых расстояний, связано соотношением:

Для кодов, обнаруживающих все трехкратные ошибки.

          количество обнаруженных ошибок

Для кодов, исправляющих двойные ошибки

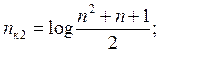
Для кодов, исправляющих тройные ошибки:

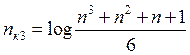
Для кодов, исправляющих S ошибок:

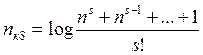
Пример:  Требуется передавать, обнаруживающим трёхкратные ошибки, все комбинации пятизначного двоичного кода. Чему равна общая длина кода ?

r – кратность обнаруживающих ошибок.

s – кратность исправляемых ошибок.

n_и = 5;     n_к = 1 + log[6 + log6] = 5

n = n_и + n_к = 10