Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 15

Недостаток: громоздкость кода и только 3-и ошибки.

2. Декодирование с проверкой на четность.

С помощью ортогональных векторов u из матрицы Н можно установить связь между составляющими векторов v.

Используя условие ортогональности:

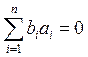
Составляющие  - берутся из матрицы Н, а  - из принятого вектора.

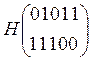       схема проверок:

На основании векторов u можно записать схему проверок

 

 

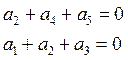
Пример: , пусть принят вектор v_x = 00110. Он имеет координаты а₁ а₂ а₃ а₄ а_5. Составим схему проверок.

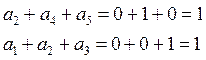
Если бы ошибок не было бы, то здесь были бы нули.

Возможность кода к исправлению ошибки можно объяснить схемой

	N символов
N-проверки	1	2	3	4	5
1		+		+	+
1	+	+	+

Следовательно, данный код может исправить во втором бите, обнаружить ошибку четвёртом или пятом бите, обнаружить ошибку в первом и третьем бите.

Для исправления всех ошибок надо, чтобы каждый бит появлялся в оригинальной комбинации строк в таблице проверки, и так будет, когда d₀=3 и добавиться ещё одна проверка.

3.  Декодирование с помощью корректирующего вектора

Составляется корректирующий вектор, принятая кодовая комбинация умножается на корректирующий вектор, если принятая комбинация без ошибок, то корректирующий вектор равен нулю (т.е. результат умножается).Если есть ошибка, то результат ненулевой, каждой ошибке ставится в соответствие свой ненулевой результат умножения.

Составляющие вектора С c₁,c₂,..,c_i представляют собой скалярное произведение принятого вектора v_x  на строки исправляющей матрицы. Вектор представляется двоичным числом С = c₁,c₂,…,c_к. Если ошибок нет, то С = 0

Рассмотрим i-ую строку полной кодовой таблицы

 - i-ая строка полная кодовая таблица

Умножим эту строку на вектор u_j, то получим

                              =0                              =0                 =0

 - в каждой строке будет одной и той же величиной для любой кодовой комбинации.

Метод декодирования состоит из следующих операций:

1)  По полной кодовой таблице и матрицы Н вычисляют корректирующий вектор С;

2)  Принятый вектор v_x умножают на векторы матрицы Н и вычисляют корректирующий вектор.

3)  Сравнивают полученные значения корректирующего вектора с имеющимся шаблоном и определяют ошибку

Пример: Нужно выбрать систему кодирования. Возьмём ту же систему кодов и H.

1. Определение шаблонов корректирующего вектора

                                                                       Векторы ошибок

шаблоны

                                          

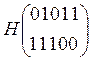
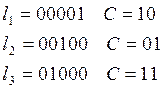
Для вектора e₁ построение шаблона.

e₁:

           e₁×u₁ = 00001×01011 = 1 Þ C₁ = 1

           e₁×u₂ = 00001×11100 = 0 Þ  C₂ = 0

Следовательно, вектору e₁ ставится в соответствие вектор С = (10)

Для e₂:

           e₂×u₁ = 00100×01011 = 0 Þ C₁ = 0

           e₂×u₂ = 00100×11100 = 1 Þ C₂ = 1

Для e₃:

           e₃×u₁ = 01000×01011 = 1 Þ C₁ = 1

           e₃×u₂ = 01000×11100 = 1 Þ C₂ = 1

Шаблоны известны на приёмной стороне ещё до посылки комбинации

2. Определение корректирующего вектора

Пусть принят вектор v_x = 01001

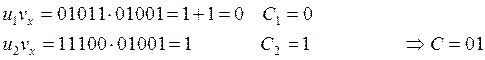
Сравниваем полученный вектор ошибки с нашим шаблоном и определяем, что это e₂.

3) Исправляем ошибку

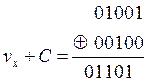, что соответствует комбинации v₃.

Можно строить образующую матрицу достаточно простым способом, например, единичной матрицей n_u ´ n_i.

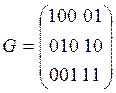 Эта матрица порождает восемь кодов, которые также позволяют обнаружить одиночную ошибку.

Преимущество кода состоит в том, что его можно легко составить, в исправляющих способностях выйгрыша нет.

Код Хэминга

Код Хэминга относится к систематическим кодам. Код позволяет обнаруживать одиночные и двойные ошибки и исправлять одиночные ошибки. Для вычисления основных параметров кода необходимо знать соответственно количество информационных разрядов n_u или количество комбинаций . Количество контрольных разрядов n_k вычисляют из соотношений