Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 3

H(x / y) = 0.3[h(0.1/0.3) + h(0.2/0.3)]+ 0.4[h(0.2/0.4 + h(0.2/0.4)] = 0.68 бит/символ

Н - характеризует потери сигналов при прохождении через канал связи.

Теорема сложения энтропий

Если две системы X и Y объединятся в одну, то энтропия объединений системы равна энтропии одной из систем плюс условная энтропия второй системы относительно первой.

H(x, y) = H(x) + H(y / x)

Доказательство этой теоремы:

Запишем H(x, y) через. математическое ожидание

H(x, y) = M[ - log p(x, y)]

По теореме умножения вероятностей

p(x, y) = p(x) * p(y / x)

log p(x, y) = log p(x) + log p(y / x)

M[x, y] = M[ - log p(x)] + M[ - log p(y / x)]

H(x, y) = H(x) + H(y / x)

Интерес представляют частные случаи:

·  Когда системы независимы, условная энтропия H(y / x) = H(y) и получаем теорему сложения энтропий H(x, y) = H(x) + H(y).

H(x, y) £ H(x) + H(y)

·  Когда состояние одной системы X полностью определяет состояние другой системы Y. В этом случае условная энтропия равна нулю.

H(y / x) = 0                   H(y, x) = H(x)

Пример: Передаются два элемента a, b. Определить количество переданной информации в случае, когда:

1) Элементы взаимозависимы и не равновероятны

p(a) = ;         p(b) = ;         p(a / a) =      p(b / a) =

                                                p(b / b) = 0       p(a / b) = 1

I = H – вероятность события а

I = H = - p(a)[ p(a / a) log p(a / a) + p(b / a) log p(b / a) ] – p(b)[ p(a / b) log p(a / b) + p(b / b) log p(b / b)] = 0.685 бит/символ .

2) не равновероятны и независимы:

p(a) = _;                p(b) =

I = - p(a) log p(a) – p(b) log p(b) = - log  - log = 0.815 бит/символ

3) элементы независимы и равновероятны:

p(a) = p(b) = ;           I = log₂ = 1

Определение информационных потерь в каналах связи

Производится с помощью вычисления условной энтропии. Составляется канальная матрица. Пусть по каналу связи источником информации передаются сигналы x₁, x₂, …, x_{m .} На другом конце канальной связи существует приёмник, который принимает сигнал y_1, y_2, …, y_m . В канале существуют помехи. Правильный приём - если послан сигнал x₁ и принят сигнал y₁. Если послан сигнал х_1, а принят y_j  - ошибка приёма.

Влияние помех описывается с помощью канальной матрицы - таблицы.

 

xi & yj	y1	y2	yi …	ym
x1	p(y1/x1)	p(y2/x1)	p(yj/x1)	p(ym/x1)
x2	p(y1/x2)	p(y2/x2)	p(yj/x2)	p(ym/x2)
xi …	p(y1/xi) …	p(y2/xi) …	p(yj/xi) …	p(ym/xi) …
xm	p(y1/xm)	p(y2/xm)	p(yi/xm)	p(ym/xm)

                                        Правильный приём

Вероятности стоящие на главной диагонали выражают правильный приём, а остальные ошибочный. Если в канале нет помех, то главная диагональ состоит из единиц, а остальные нуль. Если влияние помех очень большое, то вероятности стоящие на одной строке одинаковые. Данная канальная матрица указывает влияние помех со стороны источника сообщений, они используются для исследования помех со стороны источника.

Потери информации, которые приходятся на сигнал x₁ можно подсчитать, как условную частную энтропию.

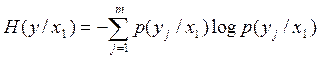 - подсчёт потерь

При передачи всех сигналов, общие потери определятся как полная условная энтропия.

их вероятности                                 потери

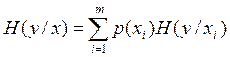
Вероятности по столбцам полную группу не образуют.

Если исследуется канал со стороны приёмника, то канальная матрица имеет другой вид:

 

xi & yi	y1	y2	yi …	ym
x1	p(y1/x1)	p(y2/x1)	p(yi/x1)	p(ym/x1)
x2	p(y1/x2)	p(y2/x2)	p(yi/x2)	p(ym/x2)
xi …	p(y1/xi) …	p(y2/xi) …	p(yi/xi) …	p(ym/xi) …
xm	p(y1/xm)	p(y2/xm)	p(yi/xm)	p(ym/xm)