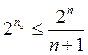Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 16

, n = n_u + n_k , n – значность кода,

Количество контрольных разрядов можно определить по таблице. Номера позиций контрольных символов выбирают по закону 2ⁱ, i = 0,1,2… Значения контрольных разрядов выбирают следующим образом.

Алгоритм:

1) Составляется вспомогательная таблица для ряда натуральных чисел в двоичной коде, Число строк в таблице n – значность кода. В каждой i –й строке вспомогательной таблицы ставится в соответствие a_i коэффициент, который участвует в проверке, a_i – коэффициенты, из которых составлена кодовая комбинация

На основании этой таблицы составляется схема проверок, которые производятся суммированием выбранных проверочных коэффициентов . Для каждой поверки выбираются свои проверочные коэффициенты. В первую проверку входят коэффициенты, которые содержат в младших разрядах единицы. Во вторую проверку входят коэффициенты содержащие единицу во втором разряде(a₂,a₃,a₆,_…). В третью проверку входят коэффициенты содержащие единицу в третьем разряде.

Схему проверок сведём в отдельную таблицу.

Количество проверок равно количеству разрядов. Контрольные коэффициенты выбираются таким образом, чтобы проверочная сумма была равна нулю. Т.е. если количество единиц чётное, то контрольный разряд нулевой, если нечётнно, то контрольный разряд равен единице.

Пример: Построить код Хэминга по комбинации

0101                             n_u = 4               n_k = 3               n_k = log(n_u + 1) + log(n_u + 1)

1,2,3                                                                             k = 7    2ⁱ = 1,3,4,8

Контрольные разряды будут занимать позиции 1,2,4.

Код Хэминга

а₁a₂a₃a₄a₅a₆a₇

k₁k₂0  k₃1  0  1              - макет

1) a₁ + a₃ + a₅ + a₇ = k₁ + 0 + 1 + 1 = 0 Þ k₁ = 0

2) a₂ + a₃ + a₆ + a₇ = k₂ + 0 + 0 + 1 = 0 Þ k₂ = 1

3) a₄ + a₅ + a₆ + a₇ = k₃ + 1 + 0 + 1 = 0 Þ k₃ = 0

Код Хэминга будет иметь вид 0100101

Декодирование кода Хэминга

В процессе декодирования производится проверка на чётность по схеме проверок и строится вектор ошибок S(S_k, …,S₁). Если проверочная сумма равна нулю, то в вектор ошибки записывается ноль иначе записывается единица. Всего делается n_k проверок. В результате первой проверки определяется составляющая S₁, последней составляющая S_k. Если принятая кодовая комбинация содержит ошибку, то в векторе S образуется число, которое указывает номер ошибочной позиции.

Пример: Послана комбинация v_k = 0100101. Принятая комбинация v_x = 0100111, т.е. имеется ошибка в шестом разряде Составим схему проверок.

1) a₁ + a₃ + a₅ + a₇ = 0 + 0 + 1 + 1 = 0 Þ S₁ = 0

2) a₂ + a₃ + a₆ + a₇ = 1 + 0 + 1 + 1 = 1 Þ S₂ = 1

3) a₁ + a₅ + a₆ + a₇ = 0 + 1 + 1 + 1 = 1 Þ S₃ = 1

S = 110 ® это двоичное число шесть, что соответствует разряду a₆, следовательно, ошибка в шестом разряде.

Для исправления одинарной и обнаружение двойной ошибки, кроме проверок по контрольным позициям проводят проверку на чётность для каждого кода. Для этого при формировании кода каждому коду в конце кодовой комбинации добавляется контрольный символ так, чтобы сумма единиц в полученной комбинации всегда была чётной.

Особенности декодирования.