Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 14

Кодовый вектор – последовательность 0-й и 1-й кодовой комбинации.

Вес кодового вектора – число единиц в кодовой комбинации.

Нулевой вектор – кодовая комбинация, состоящая из одних нулей.

n – значность кода (из скольки символов состоит кодовая комбинация);

n_u – число информационных разрядов;

n_k – число контрольных разрядов;

Пример: Для систематических кодов применяют обозначение:

Код(n, n_u)                 Код (5,3)

Построение систематических кодов производится следующим образом: в качестве первого берется нулевой вектор, затем составляется производящая матрица. Она имеет n_и – строк, n – столбцов. В качестве строк производящей матрицы берутся любые линейно независимые n-значные векторы, отстоящие друг от друга не менее, чем на заданное кодовое расстояние. Строки матрицы G – являются кодовыми векторами. Первый вектор - нулевой.

Линейно независимыми называются векторы, для которых выполняется условие:

v₁, v₂,...,v_к

v₁ + v₂ + ...+ v_к ≠ 0

Остальные кодовые векторы определяются количеством:

 где

 - всего (общее число кодовых векторов);

  - находится в производящей матрице;

1 –нулевой вектор.

Остальные кодовые векторы получаются в результате суммирования строк производящей матрицы G в различных сочетаниях.

Для обнаружения ошибок составляется множество проверочных векторов, ортогональных векторам кода. Т.е. если кодовый вектор v образован символами а₁, а₂,…, а_n, а ортогональный вектор u образован символами – b₁, b₂,..., b_n, то

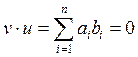
Из векторов u составляется проверочная матрица Н. Она имеет n_к – строк, n-столбцов. Строками матрицы Н являются любые линейно-независимые векторы u.

Пример: Пусть строится код (5,3) с минимальным кодовым расстоянием d₀=2. Он позволяет обнаруживать все одиночные ошибки. Составим производящую матрицу G:

                        Три строки, т.к. n_u = 3, n = 5 – столбцы

                                                                Комбинации                        Результат комбинации

1 + 3

1 + 2 + 3

2 + 3

1 + 2

Строки матрицы G

Нулевой вектор

                                                            

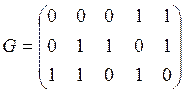
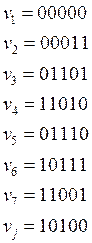
Можно было бы построить G из любой другой тройки векторов, кроме сочетаний v₂v₃v₅, v₂v₄,v₁ и т.д. (семь штук), т.к. эти сочетания линейно зависимы, т.е. v₂ + v₄ + v₇ ≠0.

Построим ортогональные векторы u (проверочные).

 Составим для векторов v₂, v₃, v_8. Эти вектора имеют минимальное количество единиц.

v₂    0 × b₁ + 0 × b₂ + 0 × b₃ + 1 × b₄ + 1 × b₅ = 0

       b₄ + b₅ = 0

v₃    b₂ + b₃ + b₅ = 0

v₈    b₁ + b₃ = 0

Для любого вектора u должно выполняться

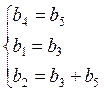
Перебирая все удовлетворяющие этим условия сочетания, получили:

u₁ = 00000

u₂ = 01011

u₃ = 10111

u₄ = 11100

Из этих векторов необходимо составить проверочную матрицу Н

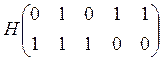    - т.к. они линейно независимы

Декодирование систематических кодов

1. Декодирование с помощью полной кодовой таблицы. Рассчитаем параметры этой таблицы

N = 2⁵ = 32 – код пяти значений

N₀ = 2³ = 8 – разрешённая комбинаяция

N - N₀=32-8=24 – запрещённая коибинация ( кодовых исправлений 24 ошибки )

Строим полную кодовую таблицу. В качестве первой строки используем разрешенные комбинации v₁ – v₈

00000	00011	01101	11010   01110   10111   11001   10100
00001 00100 01000	00010 00111 01011	01100 01001 00101	…

Общий метод декодирования состоит в следующем: Приняв некий вектор v_x, содержащий ошибку, его отыскивают в полной кодовой таблице и соотносят с тем кодовым вектором, который стоит в верхней строке этого столбца.

Пример: v_x=00111, находим в таблице и соотносят с 01 строкой, т.е. v = 00011

Достоинство метода: его универсальность, возможность применять различные стратегии.