p(a / a) = 2/3 p(b / a) = 1/3
p(a / b) = 1 p(b / b) = 0
I| = 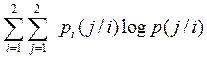 =
= 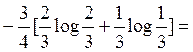 0.685 бит/символ
0.685 бит/символ
Пусть передаётся сообщение из n взаимозависимых и не равновероятных элементов.
I = n * I|
Если устранить внутренние вероятностные связи, то информация возрастёт до максимального значения Imax . При этом тоже количество информации может содержаться в сообщении из меньшего числа элементов n0.
![]() В данном случае мерой избыточности
может служить относительное число лишних элементов. Обозначим избыточность
символом D.
В данном случае мерой избыточности
может служить относительное число лишних элементов. Обозначим избыточность
символом D.
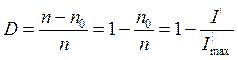 - мера избыточности
- мера избыточности
Если принять, что избыточность определяется только взаимосвязью элементов, то
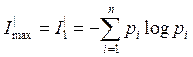
Если
принять, что избыточность определяется только распределением вероятностей, то в
качестве ![]() ,
m – количество элементов
,
m – количество элементов
Таким образом, выделяют две частных избыточности:
1) Частная избыточность, обусловленная взаимосвязью между элементами
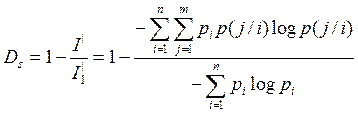
2) Частная избыточность, зависящая от распределения вероятностей
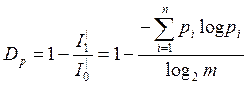 m – количество символов алфавита
m – количество символов алфавита
3) Выделяют полную информацию избыточность
D
= Dp + Ds –
DpDs ![]() Dp + Вы
Dp + Вы
Рассмотрим основные цифры и порядки для рассмотрения примера
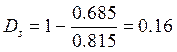 - относительная величина
- относительная величина
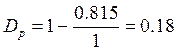 Ds * Dp = 0.03 принебрегаем
Ds * Dp = 0.03 принебрегаем
![]()
Пример избыточности в нашем языке можно проиллюстрировать следующими цифрами. Если бы все комбинации букв были возможны, то имея 30 букв, можно было бы составить 301 = 30 однобуквенных слов. 302 = 900 – двухбуквенных слова. 303 = 27 000 – трёхбуквенных слова. 304 = 810 000 – четырёх буквенных слова.
Обычный
язык содержит 50 000 слов, т.е. среднее число букв в слове, составляет примерно
3,5. В обычном в языке среднее число букв в слове семь, следовательно,
возможные комбинации 307 = 21 * 109 - столько слов можно
было бы иметь, следовательно, количество букв, которые являются словами = 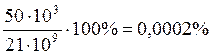 .
.
Один из методов борьбы с избыточностью применение неравномерных кодов. Метод построения оптимального неравномерного кода Шеннона - Фана. Пусть в алфавите имеется n букв и вероятности появления этих букв. Расположим эти буквы в порядке убывания их вероятностей. Затем разбиваем их на две группы так, чтобы суммарная вероятность в каждой группе по возможности была одинаковой (верхнюю группу кодируем единицей, а нижнюю нулём). Это будет первый символ кода. каждую из полученных групп делим снова на две части возможно близкой к суммарной вероятности, присваиваем каждой группе двойной символ: (один или ноль). Процесс деления продолжаем, пока не придём к первой группе.
Пример: Данный алфавит, содержит шесть букв.
|
Буква |
Вер-ть |
1 |
2 |
3 |
4 |
|||
|
a1 |
0.4 |
1 |
||||||
|
a2 |
0.2 |
0 |
1 |
|||||
|
a3 |
0.2 |
0 |
0 |
1 |
||||
|
a4 |
0.1 |
0 |
0 |
0 |
1 |
|||
|
a5 |
0.05 |
0 |
0 |
0 |
0 |
1 |
||
|
|
0.05 |
0 |
0 |
0 |
0 |
0 |
![]()
![]()
В случае равномерного кодирования потребовалось бы три бита (23 = 8).
Для данного кода
![]()
|
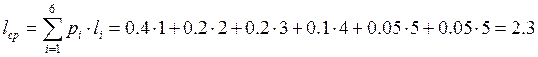 бит/символ
бит/символ
Подсчитаем энтропию данного алфавита
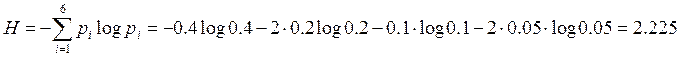 бит/сим
бит/сим
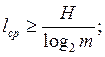 m – количество символов вторичного
алфавита
m – количество символов вторичного
алфавита
Если вторичный алфавит – двоичный, то m = 2, следовательно ![]() .
.
Пример: Задан алфавит из восьми букв и вероятности их появления. Построить оптимальный неравномерный код Шеннона-Фана.
|
Буква |
Вер-ть |
1 |
2 |
3 |
4 |
|
a1 |
0.25 |
1 |
1 |
||
|
a2 |
0.25 |
1 |
0 |
||
|
a3 |
0.125 |
0 |
1 |
1 |
|
|
a4 |
0.125 |
0 |
1 |
0 |
|
|
a5 |
0.625 |
0 |
0 |
1 |
1 |
|
a6 |
0.625 |
0 |
0 |
1 |
0 |
|
a7 |
0.625 |
0 |
0 |
0 |
1 |
|
a8 |
0.625 |
0 |
0 |
0 |
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.