Информация, язык, общество. Измерение информации. Энтропия и её свойства. Определение информационных потерь в каналах связи. Передача информации по дискретным каналам связи. Код Хэминга, страница 19

Остаток 011 110 111 101

10000    1011

1011

  01100

    1011

      1110                                              

      1011

        101

1+2      2+4      1+2+3+4

1+3      3+4

1+4      1+2+3

2+3

Обнаружение и определение ошибок

Производится по остаткам  деления принятого кодового вектора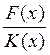.       Если в результате образовался остаток R(x) = 0, то комбинация принята без ошибок. Если есть остаток, то производят исправления. Для этого

1)  Определяют вес остатка

Если W_R  S   , где S – количество исправленных ошибок, то производят коррекцию. Для этого F(x) + R(x) и эта сумма даёт исправленную комбинацию.

Если вес W_R  S , то производят циклический сдвиг F(x) влево, образуют новую комбинацию F₁(x).

Полученную комбинацию делят на обратный многочлен

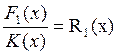- остаток

Если , то производят коррекцию F₁(x) + R₁(x), затем полученную комбинацию сдвигают вправо циклически на один разряд.

Если   , то ещё раз сдвигаем циклически влево и т.д.

Пример: Пусть посылается комбинация u(x) = 0100111 (из обратной матрицы)

Пусть принята комбинация F(x) = 1100111, содержащая ошибку в единичном разряде

U(x) = 0100111             K(x) = 1011

F(x) = 1100111             S = 1

                   

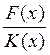
1100111   1011

1011

  1111                                 R = 101

  1011                                 W_R = 2 > S

    1001

    1011

      101

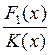
1001111   1011

1011

  1011                                 R₁ = 1

  1011                                 = 1 = S Þ можем производить коррекцию

        01

F₁(x) + R₁(x)                       1001111

                                                       1

                                           1001110

Циклически сдвигаем комбинацию вправо на один разряд 0100111 – исправляется кодовая комбинация.

Сложение двух соседних комбинаций циклического кода эквивалентно операции умножения первого слагаемого на x + 1.

     000101              две комбинации из производящей матрицы

001010               (x² + 1) * (x +1) = x³ + x +x² +1 = 001111

    001111

Образующие многочлены представляют собойьнеприводимые многочлены.

Коды, обнаруживающие трёхкратные ошибки

Методика построения следующая:

1) Выбор числа корректирующих разрядов

           n_k – количество корректирующих разрядов

Значения логарифма округряется до целых чисел в большую сторону

Пример: n_u = 2            = 4

2) Выбор образующего многочлена. Он производится исходя из следующих соображений: для обнаружения трёхкратной ошибки надо иметь d₀ = r + 1 = 3 + 1 = 4 степень обратного многочлена должна быть больше или равна четырём, т.е.

Этот многочлен получают как произведение многочлена степени (n_k - 1)т.е. 3, который позволяет обнаруживать все двойственные ошибки и многочлены первой степени (x + 1), который обнаруживают любое количество нечётных ошибок. Полученный многочлен унаследует корректирующие свойства, т.е. он будет обнаруживать одиночную и тройную ошибки, используя корректирующие свойства многочлена x + 1 и будет обнаруживать двойные ошибки, используя свойства Шеннона, например x³ + x² +1.

Произведём умножение

M₁ = x + 1

M₃ = x³ + x² + 1

M₁ x M₃ = (x + 1)( x³ + x² + 1) = x⁴ + x² + x +1 = k(x)

x³ + x³ = 0                    k(x) = 10111

x³ + x³ + x³ = x³

3) Построение образующей матрицы

Производят нахождением остатка последней строки единичной повёрнутой матрицы на обратный многочлен 100…к(х)       - методика в прошлой лекции. Второй способ умножением строки единичной матрицы на образующий многочлен. Остальные комбинации получают суммированием комбинаций строк.

4) Обнаружение ошибок производят по остаткам от деления принятого кодового вектора на образующий многочлен. Если остатки есть, то принята ошибочная комбинация.

Пример: Строим код на четыре комбинации

01 х к(х) = 01 x 10111 = 010111

10 х к(х) = 10 х 10111 = 101110

Обратная матрица

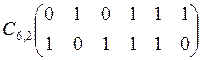
Обнаружение ошибки

1) Тройная ошибка

v₁ = 010111