Относят к группе неравномерных кодов. С помощью кодов Хафмана получают сообщения, в которых содержатся наименьшее среднее число символов на букву, т.е. это оптимизирующие коды.
Методика построения кодов следующая:
Пусть есть алфавит А, содержащий буквы
а1, а2, …, аn, вероятности появления которых р1, р2,…,
рn. Буквы алфавита располагаем в порядке
убывания их вероятностей 
.
Берем две последние буквы 
и объединяем их в одну
букву b. Получаем новый алфавит А1
а1, а2, …, аn-2 b
p1, р2,…, рn-2 pn-1 + pn
Алфавит А1 называют сжатым, полученным из алфавита А путем однократного сжатия.
Буквы алфавита А1 располагаем в порядке убывания их вероятностей. Затем проводим процедуру сжатия, получаем алфавит А2. Продолжаем процедуру сжатия до тех пор, пока у нас не останется 2 буквы.
|
Буква а1 а2 а3 а4 а5 а6 |
А Вероятность 0,4 0 0,2 10 0,2 111 0,1 1101 0,05 11001 0,05 11000 |
Сжатые алфавиты |
|||
|
А1 0,4 0 0,2 10 0,2 111 0,1 1101 0,1 1100 |
А2 0,4 0 0,2 10 0,2 111 0,2 110 |
А3 0,4 0 0,4 11 0,2 10 |
А4 0,6 (1) 0,4 (0) |
||
Процедура кодирования
Две буквы последнего алфавита кодируем 1 и 0. Затем кодируется предыдущий алфавит. Процесс кодирования закончен. Чтобы определить эффективность, надо посчитать среднее число символов на алфавит.
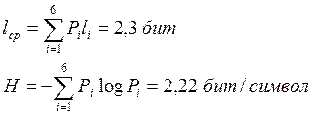
Кодирование алфавита по методу Хафмана не является однозначно определенной процедурой. Можно получать разные коды Хафмана.
Чтобы посмотреть изменение кода Хафмана, рассмотрим пример другой кодировки:
|
Буква а1 а2 а3 а4 а5 а6 |
А Вероятность 0,4 11 0,2 01 0,2 00 0,1 100 0,05 101 0,05 1010 |
Сжатые алфавиты |
|||
|
А1 0,4 11 0,2 01 0,2 00 0,1 101 0,1 100 |
А2 0,4 11 0,2 10 0,2 01 0,2 00 |
А3 0,4 0 0,4 11 0,2 10 |
А4 0,6 (1) 0,4 (0) |
||
Если посчитать 
,
то оно не изменилось 
,т.е. каким образом кодировать
роли не играет.
Процедура декодирования кодов Хафмана является однозначной.
Используя методику Хафмана, можно строить оптимальные коды, если для кодирования используется m элементарных сигналов. При построении таких кодов используется процедура сжатия, при которой сливаются каждый раз m букв алфавита. Последовательность сжатия приводит к алфавиту из m букв.
Число букв исходного алфавита n должно быть представляемо n = m + k *(m -1), k – целое число. Этого условия всегда можно достичь, если ввести в исходный алфавит фиктивные буквы, вероятность которых равна нулю.
Дан алфавит из 6 букв с вероятностями. Построить троичный код Хафмана 0, 1, 2.
Требуемое число букв:
n = 3 + k * (3 - 1),
k = 1 n = 5
k = 2 n = 7
не хватает одной буквы а7 с вероятностью равной нулю
|
Буква а1 а2 а3 а4 а5 а6 а7 |
А Вероятность 0 0,4 2 0,2 10 0,2 11 0,1 120 0,05 121 0,05 122 0 |
С ж а т и е |
|
|
А1 0 0,4 2 0,2 10 0,2 11 0,1 12 0,1 |
А2 0,4 (0) 0,4 (1) 0,2 (2) |
||
Подсчитаем энтропию
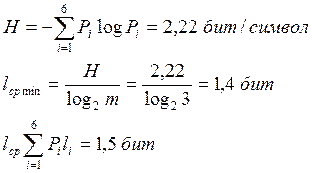m – количество символов
Существует еще одна методика
|
|
|
 |
|
 |
|||
|
|||
1
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.