Государственный комитет Российской Федерации
по высшему образованию
Новосибирский государственный технический университет
РАДИОАВТОМАТИКА
Методические указания
к индивидуальной работе для студентов 1У курса
специальности "Радиотехника"
дневного отделения
Новосибирск
1995
Составил канд. техн. наук, доц. С. Е. Лявданский
Рецензент д-р техн. наук, проф. Т.Б. Борукаев
Работа подготовлена кафедрой радиоприемных
и радиопередающих устройств
©
Новосибирский государственный технический университет, 1995
Тема 6. КАЧЕСТРО РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ РАДИОАВТОМАТИКИ
6. 1. Общие понятия и определения
Качество регулирования - важнейшая характеристика автоматической системы. Вопрос о нем рассматривается проектировщиком системы сразу после проверки устойчивости, ибо, не обеспечив устойчивости, говорить о качестве не имеет смысла.
Понятие качества регулирования автоматической системы довольно многопланово. В различных ситуациях проектировщика и эксплуатационника системы могут интересовать различные аспекты качества регулирования. Выделим три из них.
1. Качество
регулирования в установившемся и вынужденном
режимах.
2. Качество регулирования в переходном режиме.
3. Качество
регулирования при воздействии на систему
случайных процессов.
В данной теме рассматривается лишь первый аспект проблемы -качество регулирования при воздействии на систему детерминированного сигнала, который может быть представлен аналитической Функцией, абсолютно дифференцируемой на любом отрезке. Например:
x(t)= At³+Bt²-ct; x(t)= B Cos Wt
x(t)= Ae α1t +Be –α2t
и т. п.
Под качеством регулирования в этом случае подразумевают величину ошибки регулирования, причем, чем она меньше, тем выше качество. Ошибкой считается отклонение реального состояния регулируемого параметра объекта регулирования от заданного. Например, пусть мы имеем электронно управляемый ВЧ генератор, частота которого должна изменяться по закону внешнего управляющего сигнала f1 (t). Реальное значение частоты генератора, как правило, не будет точно копировать закон f1 (t), оно будет описываться другой функцией f2 (t). В этом случае ошибкой регулирования будет считаться разница
ξ(t)=f1 (t)-f2 (t)
Замкнутые системы радиоавтоматики построены таким образом, что в их структурной схеме обязательно присутствует главный сумматор системы, являющийся по существу вычитателем. Именно на него возлагается функция выделения разницы между действительным и требуемым значениями регулируемого параметра объекта регулирования.
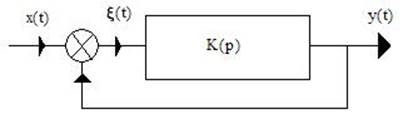
Рис. 6.1
На рис. 6.1 показана простейшая структура следящей системы, где К(р) - передаточная функция разомкнутой системы; здесь х(t) – управляющее воздействие; у(t) - результат регулирования.
Сигнал на выходе главного сумматора ξ (t) является сигналом ошибки.
6. 2. Методы определения ошибки регулирования
Возможны различные подходы к отысканию функции ξ (t) при заданной структуре системы и управляющем воздействии X (t). Отметим некоторые из них.
6. 2.1. Запись дифференциального уравнения системы и подстановка в него ожидаемого решения в виде некоторой функции с неизвестными коэффициентами, с последующим определением этих коэффициентов
Пример 6. 1. Имеется
система, состоящая из двух инерционных
звеньев:
K(p)=![]()
Сигнал управления х(t) описывается функцией
X(t)=At
Требуется определить сигнал ошибки ξ (t).
Решение. Запишем очевидные соотношения, вытекающие из рис.6.1.
ξ (t)=X(t)-Y(t),
где y(t) – выходная функция системы; x (t) – задающее внешнее воздействие.
Запишем дифференциальное уравнение замкнутой системы, для чего сначала необходимо получить его коэффициенты. Как известно, коэффициенты дифференциального уравнения и коэффициенты передаточной функции системы - это одни и те же числа. Поэтому записываем передаточную функцию замкнутой системы:
Ф(p)=![]() (6.1)
(6.1)
Если обозначить коэффициенты числителя индексами B, а коэффициенты знаменателя индексами A, то
в0 = к; в1 = в2 + … вк = 0;
а0 = 1+ к; а1 = Т1+Т2; а2 = Т1Т2;
а3 = а4=… ак = 0.
Отсюда дифференциальное уравнение замкнутой системы:
![]() (6.2)
(6.2)
Для подстановки в уравнение (6.2) необходимо синтезировать ожидаемое решение у(t) в виде полинома с неизвестными коэффициентами
![]()
Тогда
![]() ;
; ![]()
Подставляя x(t), y(t), dy (t)/dt в уравнение (6.2), получаем:
(Т1+Т2)C1 + (1+К)(С0 + С1t) = КАt. (6.3)
Неизвестные коэффициенты С0 и С1 можно получить, приравнивая в левой и правой частях слагаемые с одинаковыми степенями t:
(1+К)С1t = КАt,
откуда:
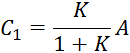
(Т1 + Т2)С1
= - (1+К) С0;
![]()
Подставляя полученные С0 и С1 в ожидаемое решение y (t), получаем
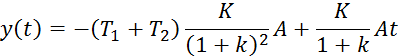
Поскольку ξ (t) = x(t) – y (t), имеем окончательно:
ξ![]()
![]() (6.4)
(6.4)
Полученное выражение показывает, что ошибка регулирования содержит ослабленную в (1+К) раз функцию входного сигнала х(t) и дополнительную постоянную составляющую
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.