Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 6

выходном сигнале будет уплощение вершин гармонического сигнала (рис. 7.1,б) и при симметричности нелинейной характеристики поя­вятся высшие нечетные гармоники. Будет при этом, конечно, и первая гармоника  V₁вых. Чтобы отразить факт зависимости Кн₁ от амплитуды входного сигнала, его обозначают

Kн₁ (A),

где А – амплитуда входного гармонического сигнала.

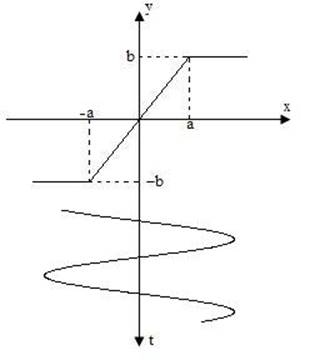
                    а                                                                 б

Рис. 7.1

Для безреактивкых  нелинейных  звеньев,   где нет частотной за­висимости характера вносимых искажений,   такого обозначения доста­точно. Для реактивных же звеньев, в которых характер искажений вы­ходного сигнала зависит не только от амплитуды,   но и  от  частоты входного гармонического сигнала, вводят обозначение

Кн (А, W).

Примером такого звена может служить полупроводниковый диод ва­рикап, совмещающий в себе нелинейную вольт-амперную характеристику открытого р-n перехода и нелинейную барьерную емкость диода в запертом состоянии. Будем считать для упрощения изложения, что в рамках данной темы мы имеем дело с безреактивными нелинейными звеньями, т. е. будем обозначать коэффициент передачи по первой гармонике как

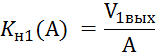
Естественно, что для нахождения аналитических зависимостей  Кн₁ (А)   различных нелинейных звеньев необходимо разложить в ряд Фурье функцию,   описывающую выходной сигнал, и взять из него только пер­вую гармонику. В табл. 7.1 приведены данные для 7 типовых нелиней­ных звеньев,   где показаны формы характеристик и аналитические

Таблица 7. 1

выражения для Кн₁. С сохранением нумерации табл. 7. 1 названия нелинейных звеньев следующие:

звено 1 – «насыщение»;

звено 2 – «зона нечувствительности»;

звено 3 – «зона нечувствительности с насыщением»;

звено 4 – «3-позиционное реле с гистерезисом»;

звено 5 – «2-позиционное реле с гистерезисом»;

звено 6 – «2-позиционное реле без гистерезиса»;

звено 7 – «3-позиционное реле без гистерезиса».

Как видно из аналитических зависимостей табл. 7.1, у звеньев с неоднозначными характеристиками (4, 5) в выражениях для Кн₁ имеется мнимая часть, что говорит о наличии фазовых сдвигов между первой гармоникой выходного сигнала и входным гармоническим сигналом. Для остальных звеньев фазового сдвига нет, т.е. максимум первой гармо­ники выходного сигнала совпадает с максимумом входного сигнала.

Интерес представляет то, что фазовые сдвиги для звеньев 4, 5 зависят от амплитуды А. Например, для звена 5

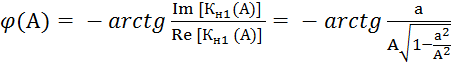
откуда видно, что при А=а φ(А)=-π/2, а при увеличении A фазовый сдвиг

должен уменьшаться. В пределе, при А → ∞ φ(А) → 0. В этом легко убедиться, рассмотрев рис. 7. 2, а  и  7. 2, б где видно, что при  А = а  прямоугольный сигнал  выхода сдвинут  относительно входного сигнала ровно на 90⁰ , а максимум первой гармоники, как известно, будет совпадать с  серединой  импульса на выходе (первая гармоника помечена  пунктиром). При А > а (рис. 7.2, 6) импульс на выходе уже сдвинут по фазе меньше 90⁰ относительно входного сигнала. По аналитическим  выражениям табл. 7.1 можно построить графики для модуля и  фазы  коэффициента передачи  по первой гармонике Кн₁(А). Такие данные приведены в табл. 7. 2. Представляют интерес зависимости для нелинейности «трехпозиционное реле с гистерезисом (звеном 4)».   Они называют коэффициентом возврата реле. Хорошо видно, что при λ → 1, когда гистерезис исчезает, звено 4 превращается в звено 7 и фазового сдвига вообще нет. При λ → 0,   когда      а₂ >> а₁, фазовый сдвиг максимален для данного эвена, но он не достигает -90°,а значительно меньше. Для этого достаточно рассмотреть рис. 7.3, где взят именно случай а₁ >> а₁ и А = а₂. Даже при А = а₂ фазовый сдвиг немного не достигает -45⁰ и может достигнуть этого значения только при а₁ → 0.