Идея метода очень проста: разложить передаточную функцию Kξx(р) в ряд по степеням комплексной переменной р, а затем, записав в операторной форме дифференциальное уравнение системы, обратным преобразованием Лапласа обеих его частей перейти к традиционной форме записи через производные.
Рассмотрим эту идею более подробно. Передаточная функция может быть записана по формуле (6.9), но для удобства разложения в ряд ее необходимо представить в виде дробно-рациональной функции параметра р, т. е. в виде отношения двух полиномов. Интересной особенностью функции Кξх(р) является тот факт, что она представляет собой отношение двух характеристических полиномов: разомкнутой системы А(р) и замкнутой системы G(р). В самом деле, если обозначим передаточную функцию разомкнутой системы в виде
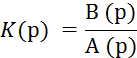
то знаменатель этой передаточной функции будет называться характеристическим полиномом разомкнутой системы.
С другой стороны, передаточная функция замкнутой системы тоже имеет свой знаменатель:
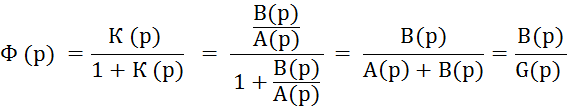
Полином G (р) называется характеристическим полиномом замкнутой системы. Обратим внимание: это сумма числителя и знаменателя передаточной функции разомкнутой системы К(р). Теперь, переходя к формуле (6.9), можно записать:
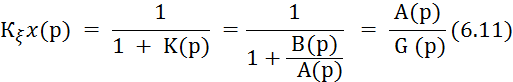
что и является отношением двух характеристических полиномов.
Отношение этих полиномов можно представить в виде некоего третьего полинома, так называемого полинома ошибки с пока что неизвестными коэффициентами:
![]() (6.12)
(6.12)
В принципе, этот полином бесконечен, так как в общем случае невозможно ожидать, чтобы два различных полинома разделились без остатка.
Коэффициенты полинома S0, S1, S2, … называются коэффициентами
ошибки.
Формулу (6.12) можно записать в более удобном виде. Так как передаточная функция есть отношение изображений двух сигналов, то
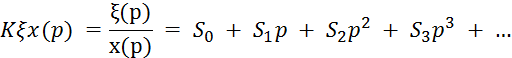
Записав это в одну строку, получим
ξ (р) = x(р)(S0 + S1p + S2p2 + S3p3 + ...),
или, переходя от операторной (символической) формы записи дифференциального уравнения к классической, получаем:
![]() (6.13)
(6.13)
Таким образом, если определить неизвестные пока коэффициенты ошибки S0, S1, S2, S3, ..., то искомая ошибка регулирования записывается в аналитической форме через входной сигнал х(t) и его производные. Это настолько удобно, что не следует жалеть усилий для определения коэффициентов ошибок.
Самый удобный способ определения коэффициентов ошибки – выразить их через известные коэффициенты характеристических полиномов А (р) и G (р).
Запишем эти полиномы в виде:
A(p)=Cnpn + Cn-1pn-1 + ... C1p + C0;
G(p)=Anpn + An-1pn-1 + A1p + A0 (6.14)
Эти записи показывают, что порядок характеристических полиномов замкнутой и разомкнутой систем одинаков. Это не случайно. Если вернуться к формуле (6.11), то видно, что в G (p) = A(p) + B(p). Ясно, что порядок полинома G (р) будет определяться порядком того полинома A(р) или В (р), который содержит переменную р в более высокой степени. Как известно, В(р) - числитель передаточной функции К (р), а А(р) h ее знаменатель.
Для всех практически встречающихся автоматических систем порядок полинома A(р) выше, чем полинома В(р), так как наиболее часто встречающиеся структурные звенья: инерционные, интегрирующие, колебательные - имеют порядок р в знаменателе своих передаточных функций выше, чем в числителе. Поэтому можно считать, что порядок полинома G (р) определяется порядком полинома A(р). Возвращаясь к формуле (6.12) и подставляя туда (6.14), путем деления двух полиномов легко найти коэффициенты третьего. В частности,
![]() ;
; ![]() ; (6.15)
; (6.15)
![]() ;
; ![]()
и т. д.
Здесь: А1, А2, А3, ... - коэффициенты полинома G(р); С0, С1, C2 ... - коэффициенты полинома А(р).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.