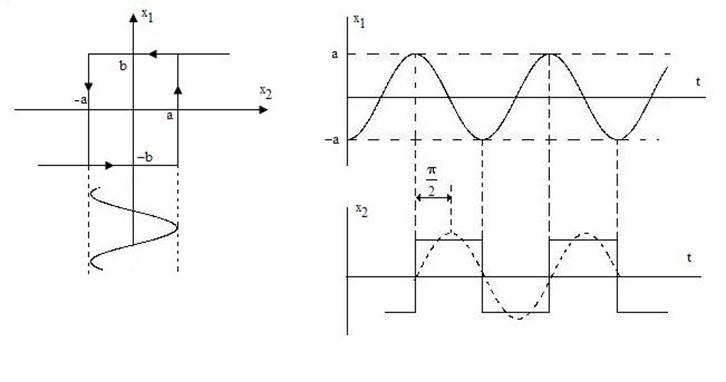
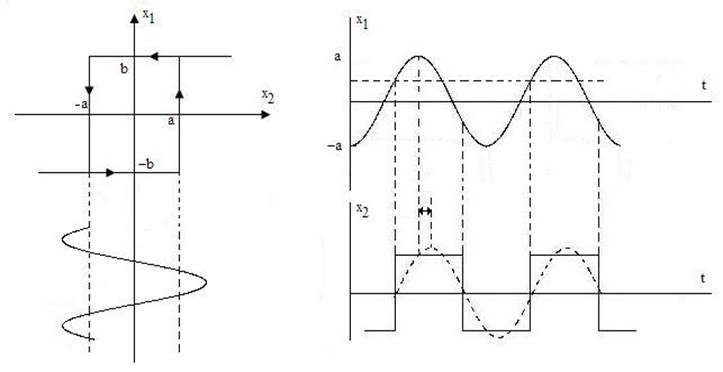
Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 7

Таблица 7. 2

Таблица 7. 3

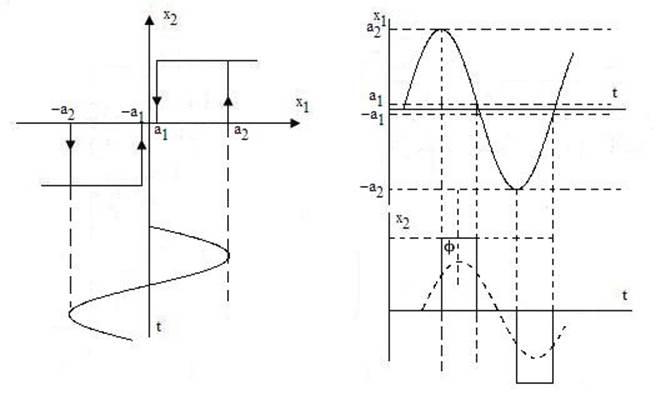
Рис. 7. 3

Зависимости Кн₁ (А) и φ (А) в табл. 7. 2 построены без соблюдения масштаба, приближенно, лишь с сохранением характера этих зависимостей. Часто этого бывает достаточно, например для решения воп­роса о возможности или невозможности автоколебаний в нелинейной системе, что является уже предметом изучения следующей темы 8. В рамках же темы 7 интересно будет рассмотреть, не прибегая к получению аналитических зависимостей, характера кривых Кн₁ (А) для не­которых нелинейных звеньев, не входящих в перечень рассмотренных выше 7 звеньев.

Пример 7.1. Звено с характеристикой рис. 7. 4  Построим зависи­мость Кн₁(А) и ее годограф. Как видно из рис. 7. 4, при А < а, звено является линейным и его коэффициент   передачи равен tgα_1. При А>а₁ будет происходить   снижение Кн₁(A), как у звена "насыщение".

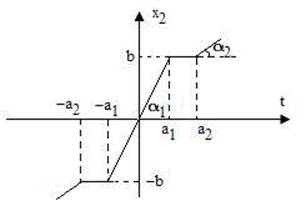
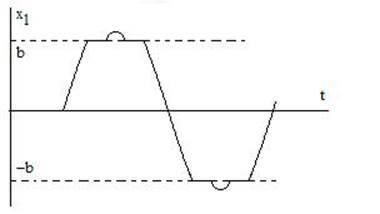
                          Рис. 7. 4                                         Рис. 7. 5

Однако после достижения амплитудой входного сигнала уровня а₂ в выходном сигнале появятся заостренные вершины (рис. 7. 5) и коэф­фициент Кн₁ (A) вновь начнет увеличиваться.

При этом увеличение Kн₁ при А → ∞ будет происходить до зна­чений Кн₁ (∞) = tg α₂.

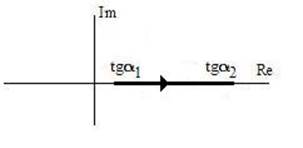
Соответствующая зависимость Кн₁ (A) показана на рис. 7. 6,а, а на рис. 7.6,б - годограф Кн₁ (А). Поскольку φ(А) = о, годограф расположен на вещественной оси.

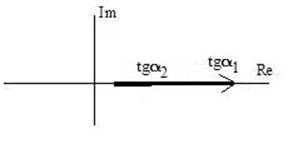
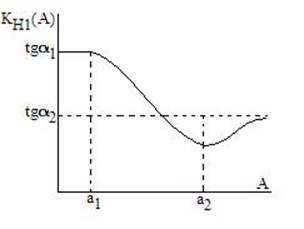
Рис. 7.6

Пример 7.2. Звено с характеристикой рис. 7. 7.

α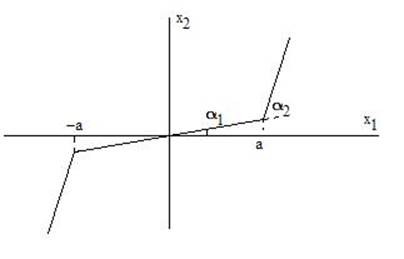₂=89⁰30^′

Рис. 7. 7

Данное звено  при  малых  амплитудах А напоминает звено предыдущее (рис. 7. 4), но при А > а  наклон   характеристики резко увеличивается. Поэтому при А → ∞Кн₁ (А) также стремится к большому числу (tg 89⁰30').

На рис.   7.8,а показана зависимость Кн₁ (А), а на рис. 7. 8,б - годограф.   Поскольку звено имеет однозначную характеристику, φ (А)=0.

                       а)                                                                   б)

Рис. 7.8

Задачи для решения в аудитории

Задача 7.1. Задана характеристика нелинейного звена (рис. 7.9).

Зарисовать вид характеристик Кн₁ (А), φ (А) и годограф Кн₁ (А) (качественно, без вычислений).

Задача 7. 2. Вид характеристики (рис. 7.10). Задание аналогично задаче 7.1.

Задача 7. 3.   Годограф Кн₁ (А) (рис.   7.11).   Нарисуйте характеристику нелинейного звена.

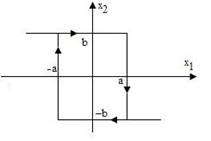
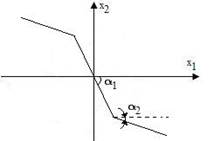
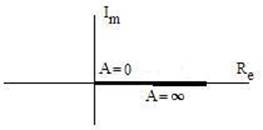
          Рис. 7. 9                               Рис.7.10                              Рис.7. 11

Тема 8. УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ И

УСТОЙЧИВОСТЬ АВТОКОЛЕБАНИЯ

Под устойчивостью нелинейных систем подразумевают отсутствие в ней  автоколебаний и устойчивость обычного равновесного состояния. Говоря об устойчивости автоколебаний, имеют в виду такой их режим, который