Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 10

Пример 8. 3.  Линейная часть системы имеет передаточную функцию

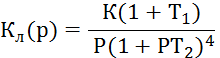
т. е., одно интегрирующее звено, одно форсирующее и четыре инерци­онных с постоянными времени Т₂. Характеристика нелинейной части системы приведена на рис. 8. 3.

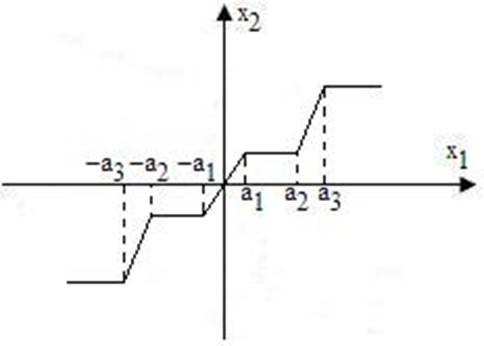
Рис. 8. 3

Возможны ли автоколебания?

Диаграмма Гольдфарба показана на рис. 8. 4. Здесь коэффициент усиления линейной части выбран таким, чтобы было 3 пересечения го­дографа Кл(iw) с годографом - 1/Кн₁ (А) нелинейной части. Эти пе­ресечения на одной частоте wо, но c разными амплитудами A₁, А₂, A₃,

причем А₃> A₂> A₁.

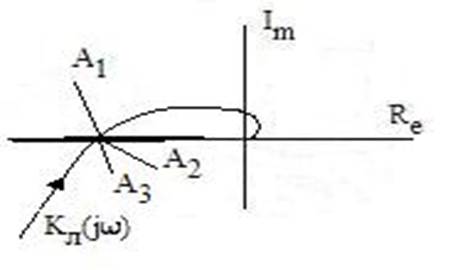
Рис. 8. 4

В такой ситуации мы имеем две точки устойчивых автоколебаний при А=А₁, А=А₃ и одну точку неустойчивых автоколебаний при А=А₂. Поскольку точек устойчивых автоколебаний все же две, возникает вопрос: при какой амплитуде будет происходить автоколебание? Ответ простой: все зависит от начальных условий. Если на систему подать питание и не подвергать ее никаким входным воздействиям, возникнет автоколебание в "мягком" режиме, дорастет до амплитуды А₁ на входе нелинейного эвена   а₂ >А> а₁ (см. рис. 8.3) и это автоколебание бу­дет устойчиво. Если попытаться внешним воздействием "выбить" систему из этого устойчивого автоколебания, то при слабых внешних воздействиях это не удастся сделать, а при сильных - удастся. В частности, если приложить внешнее воздействие большой амплитуды, то можно вывести систему на второй устойчивый режим автоколебаний с амплитудой А₃ и оно будет устойчивым. Но если отключить источник питания, а потом вновь включить, возврата ко второму устойчивому режиму с амплитудой А₃ не будет, а зародятся автоколебания первого устойчивого режима с амплитудой А₁. Здесь можно говорить о "мяг­ком" режиме самовозбуждения с амплитудой А₁ и "жестком" режиме воз­никновения автоколебания с амплитудой А₃. Следовательно, в данной системе одновременно не может быть автоколебаний с двумя амплиту­дами А₁ и А₃, а только что-то одно. Что касается автоколебаний с амплитудой А₂, то, несмотря на наличие при А=А₂ и баланса фаз, и баланса амплитуд, такое автоколебание существовать сколь-либо долго не может. Обязательно при малейшей флуктуации амплитуды ав­токолебание перейдет либо к амплитуде А₁, либо к А₃.

Все сказанное выше гораздо нагляднее можно продемонстрировать фазовым портретом данной системы, как, впрочем, и некоторых других примеров.

8. 2. Связь между диаграммой Д. С. Гольдфарба и фазовым портретом системы

Как известно, фазовый портрет системы - это семейство фазовых траекторий, зарисованных для различных начальных условий на фазовой плоскости. В частности, для устойчивых систем все фазовые тра­ектории стремятся в точку устойчивого равновесия (рис. 8.5,а), тогда как в системе с устойчивым автоколебанием на фазовом портрете имеется замкнутый   устойчивый предельный цикл, к которому асимп­тотически приближаются все рядом лежащие фазовые траектории (рис.8.5.б). Интересно то, что предельных замкнутых циклов может быть несколько - по количеству пересечений годографов на диаграмме Гольдфарба. При этом для каждой точки пересечения на диаграмме Гольдфарба, соответствующей устойчивому автоколебанию, присутству­ет устойчивый предельный замкнутый цикл на  фазовом  портрете.

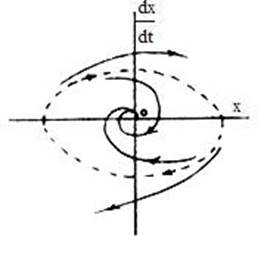а)                             б)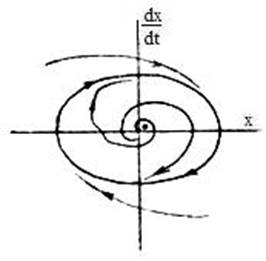

Рис. 8. 5

Он обычно рисуется сплошной замкнутой линией в виде эллипса или ок­ружности (в частном случае). Что касается точек пересечения годог­рафов, обозначающих наличие неустойчивых автоколебаний, то на фа­зовом портрете им соответствуют замкнутые неустойчивые предельные циклы, обычно рисуемые в виде пунктирных замкнутых кривых. С них как бы "скатываются" в разные стороны, рядом лежащие фазовые траек­тории, т.е., без посторонней вынуждающей силы (скажем, внешнего генератора гармонического колебания) по пунктирной траектории изображающая точка фазового портрета двигаться ощутимое время не может. Рассмотрим несколько примеров.