Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 11

Пример 8.4. Рассмотрим фазовый портрет системы с диаграммой Гольдфарба по рис. 8.1 из примера 8.1. Там мы имеем единственное пересечение годографов, причем оно соответствует устойчивому авто­колебанию. Фазовый портрет такой системы изображен на рис. 8.5,б. Все траектории стремятся к устойчивому замкнутому циклу как изнут­ри его, так и снаружи.

Пример 8.5. Вернемся к рассмотрению диаграммы Гольфарба рис. 8.2, где имеются две точки пересечения годографов. Фазовый портрет такой системы представлен на рис. 8. 6. На нем очень хорошо просматривается выход изображающей точки по спиральной траектории на устойчивый  предельный цикл с амплитудой А₁.   Если принудительно поместить рабочую точку в область между двумя предельными циклами, а затем убрать внешнее воздействие, фазовая траектория снаружи вернется на устойчивый замкнутый цикл. И только если поместить рабочую точку за пределы второго, неустойчивого замкнутого цикла, то фазовая траектория устремится в бесконечность. Она не сможет преодолеть неустойчивый замкнутый цикл с амплитудой А₂ и попасть на устойчивый с амплитудой А₁. Так что неустойчивый замкнутый пре­дельный цикл является для фазовых траекторий как бы непреодолимым "водоразделом". Преодолеть его можно только с помощью внешнего ге­нератора (внешней силы).

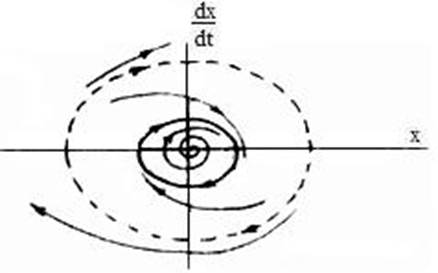
Рис. 8.6

Пример 8.6. Рассмотрим систему с диаграммой Гольдфарба по рис. 8.4. Здесь три точки пересечения годографов, причем две из них соответствуют наличию устойчивых автоколебаний. Фазовый портрет представлен на рис. 8.7. На нем видны два устойчивых предельных цикла с амплитудами А₁ и А₃ и один неустойчивый с амплитудой А₂. Общее число замкнутых циклов соответствует числу пересечений годо­графов на диаграмме Гольдфарба.

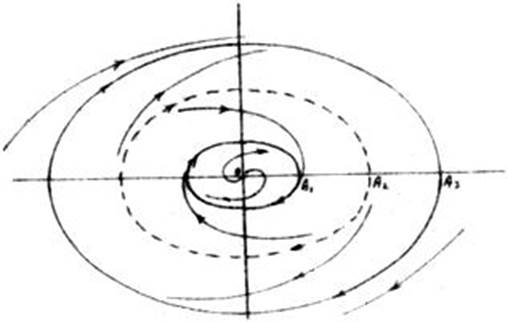
Рис. 8. 7

8. 3. Выводы

1. Если годографы на диаграмме Л. С. Гольдфарба не пересека­ются, то нелинейная система абсолютно устойчива и в ней не могут существовать автоколебания.

2. Если годографы пересекаются, то система не является устой­чивой и в ней могут существовать автоколебания. Они могут быть как устойчивыми, так и неустойчивыми, но в любом случае систему устой­чивой считать нельзя.

3. Между диаграммой Л. С. Гольдфарба и фазовым портретом системы имеется взаимосвязь. Каждой точке пересечения годографов на ди­аграмме Гольдфарба соответствует замкнутый предельный цикл на фазовом портрете, который может быть как устойчивым, так и неустойчивым. Это зависит от характера пересечения годографов и удовлетворения условия Гольдфарба для устойчивости автоколебаний.

4. На фазовом портрете предельные замкнутые циклы перемежа­ются. Любые два устойчивых замкнутых цикла разделены неустойчивым, и наоборот.

8. 4. Задачи для решения в аудитории

Задача 8.1. Линейная часть нелинейной системы

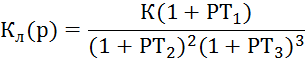
Нелинейная часть имеет характеристику, показанную на рис. 8.8. Возможны ли автоколебания и как выглядит фазовый портрет?

Задача 8.2. Линейная часть системы:

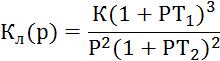
Нелинейная часть задана характеристикой, приведенной на рис. 8.9. Возможны ли автоколебания и как выглядит фазовый портрет?

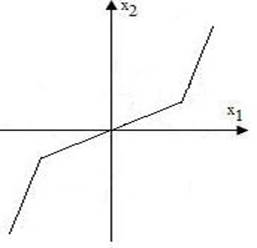
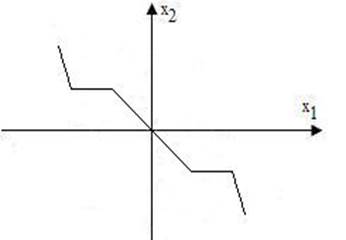
Рис.8.8                                                                       Рис. 8.9

Задача 8. 3. Задана диаграмма Гольдфарба (рис. 8.10). Напишите передаточную функцию линейной части и зарисуйте форму характеристики нелинейного звена.

Задача 8. 4. Фазовый портрет системы показан на рис. 8.11. Пред ложите вариант структуры системы и ее диаграммы Гольдфарба.

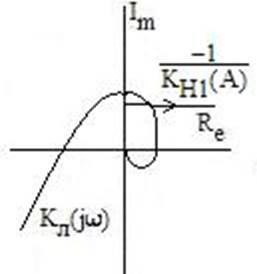
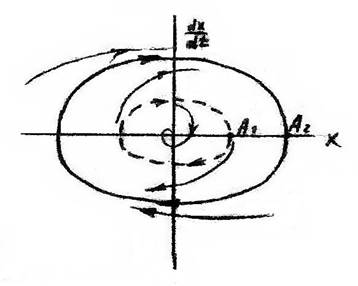
             Рис. 8. 10                                                              Рис 8.11