Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 9

Совместное изображение на одной координатной системе годогра­фов Кл(iw) и - 1/Кн₁(А) часто называют диаграммой Гольдфарба. Поскольку здесь используется коэффициент передачи нелинейного зве­на Кн₁(А) по первой гармонике, правило, при котором можно поль­зоваться гармонической линеаризацией, остается в силе. Это значит, что анализ по Гольдфарбу будет справедлив только тогда, когда ли­нейная часть системы имеет характеристику типа "фильтр нижних частот", т.е. на высоких частотах имеется спад частотной характе­ристики, обеспечивающий подавление высших гармоник частоты автоко­лебаний. Конечно, может возникнуть       вопрос: "Может же быть так, что и при наличии линейной части с    характеристикой типа ФНЧ первая гармоника будет не очень высокой частоты и в полосу пропускания

ФНЧ войдут и вторая и даже третья гармоники?" Обычно такого не происходит. Ведь если возникают автоколебания, значит, в линейной части уже накоплен значительный фазовый сдвиг, а это бывает уже на скате АЧХ, так что вторая и высшие гармоники оказываются сущест­венно подавленными. Поэтому при исследовании автоколебаний в нели­нейной системе условие наличия ФНЧ в линейной части оказывается достаточным для правомочности использования понятия гармонической линеаризации.

Пример 8.1. Пусть линейная часть нелинейной системы содержит 3 инерционных звена, а нелинейная часть имеет характеристику типа "насыщение". Тогда диаграмма Гольдфарба будет выглядеть следующим образом (рис. 8.1). Если коэффициент усиления линейной части до­статочен для того, чтобы годографы пересеклись, как и показано на рис. 8.1, то в системе будут автоколебания, причем устойчивые, так как годограф нелинейной части - 1/Кн₁ (А) в  точке пересечения по-

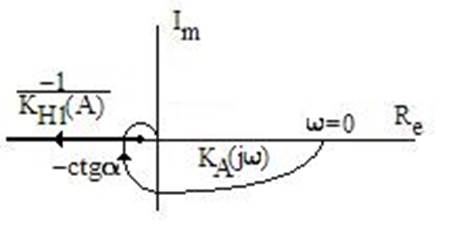
Рис. 8. 1

кидает   пределы   комплексной плоскости, очерченные годографом линей­ной части К_л(iw). На этом примере   очень наглядно можно показать, почему правило   Гольдфарба для устойчивости автоколебаний именно такое. В самом деле, для баланса амплитуд   автоколебаний в   системе необходимо, чтобы любая флуктуация   коэффициента   передачи линейной части системы   компенсировалась обратным по   закону изменением К_н1(А) нелинейной части. В данном случае это   имеет место. Так если, например, коэффициент   усиления линейной части по какой-то     причине уменьшится, то, чтобы не исчезли автоколебания,   необходимо увели­чить коэффициент передачи Кн₁(А) нелинейной части. Точно так и происходит (см. табл. 7.2). В свою очередь для уменьшения Кн₁(А) значение обратной функции должно увеличиться. Вот почему ее годограф удаляется от начала координат. А наличие знака "минус" от­брасывает этот годограф на отрицательный отрезок вещественной оси, и он уходит в бесконечность при А →∞ (сама функция Кн₁ (А) при этом стремится к нулю).

Пример 8. 2. Пусть линейная часть нелинейной системы  содержит
одно интегрирующее и три инерционных звена, т. е.

а нелинейная часть имеет характеристику по рис. 7. 4 из примера 7.1.            

Возможны ли автоколебания?

Диаграмма Гольдфарба для данного примера приведена на рис. 8. 2.

Значение коэффициента усиления линейной части  выбрано  достаточно

большим для того,   чтобы годографы линейной и нелинейной части                 

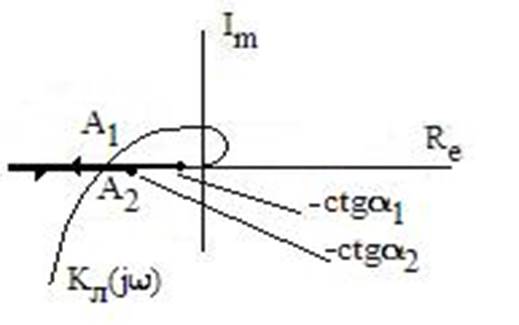
Рис. 8. 2

пересекались дважды, при А = А₁ , и  А = А₂. Согласно правилу Гольд­фарба автоколебание   будет устойчивым с амплитудой А₁. При А = А₂ автоколебание возможно лишь теоретически, так как любая флуктуация коэффициента усиления линейной части будет усиливаться характеристикой нелинейной части (а должна подавляться). В этом случае автоколебание либо "перескочит" в точку устойчивых автоколебаний с ам­плитудой А = А₁, либо устремится в бесконечность, в зависимости от направления   первичной  флуктуации,   "выбивающей" автоколебание из точки А = А₁.     Точка А₁ является точкой  устойчивых автоколебаний. Точка А₂ является точкой неустойчивых автоколебаний.   Что касается частоты автоколебаний, то, поскольку оба пересечения происходят на отрицательном отрезке вещественной оси,   частота обоих  автоколебаний (устойчивого и неустойчивого) будет одинаковой и определится по годографу линейной части. Конкретно, это будет частота w_o, на ко­торой φ(w) линейной части равен (-180°).