Качество регулирования в линейных системах радиоавтоматики. Гармоническая линеаризация. Устойчивость нелинейных систем и устойчивость автоколебания, страница 4

Полученные формулы для коэффициентов ошибки интересны не только тем, что позволяют их рассчитать, но и тем, что открывают ясный путь к пониманию сущности астатизма. Они позволяют понять, почему наличие именно интегрирующих звеньев превращает систему в астатическую и уменьшает ошибку регулирования.

Рассмотрим несколько примеров.

Пример 6. 3. Возьмем статическую систему

Для такой системы

C₀ = 1;            С₁ = T₁ + T₂;          С₂ = T₁T₂;

A₀ = 1 + K;          A₁ = T₁ + T₂;       A₂ = T₁T₂

Ни один коэффициент не равен нулю или бесконечности. Следовательно, как видно из (6.15), все коэффициенты ошибки отличны от нуля.

Тогда в формуле (6.13) присутствуют все слагаемые и даже при постоянном воздействии на входе системы x(t) = A ошибка ξ (1) бу­дет конечной, не равной нулю:

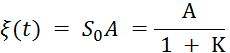
Пример 6. 4. Превратим систему в астатическую 1-го порядка:

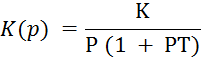
A (p) = P + P²T; С₀ = 0; С₁ = 1; С₂ = T;

G (p) = K + P + P²T; A₀ = K; A₁ = 1;  A₂ = T

Наличие интегрирующего звена приводит к отсутствию в знаменателе свободного члена не содержащего р. Отсюда - равенство нулю коэффициента С₀ и, как следствие, коэффициента S₀. Остальные коэффициенты С₁, C₂ не равны нулю, поэтому и S₁, S₂, ... тоже не равны нулю. Теперь, при подаче на вход системы постоянного воздействия, ошибки не будет:

ξ (t)=S₀A=0A=0

При подаче на вход линейно возрастающей функции х(t)=Аt ошибка будет, но она будет постоянной:

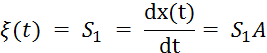
Пример 6. 5. Увеличим астатизм системы, добавив еще одно интегрирующее звено:                                    

                                                           T₁>T₂

                                                                           (для устойчивости системы)         

A (p) = P² + P³T₂;   C₀ = C₁ = 0;   C₂ = 1;     С₃ = T₂;

G(p) = K + KpT₁ + P² + P³T₂;  A₀ = K; A₁ = KT₁;  A₂ = 1;  A₃ = T₃.

Если воспользоваться формулами (6.15), то легко видеть, что два первых коэффициента ошибки равны нулю и в формуле (6.13) уже будут отсутствовать первые два слагаемых. Теперь при подаче на вход сигнала  x(t) = At ошибка будет равна нулю.

Таким образом, наблюдается очень интересная закономерность: с возрастанием порядка астатизма исчезают, начиная с S₀, коэффициенты ошибки, а в формуле (6.13) исчезают слагаемые, начиная с пер­вого. Однако не следует увлекаться астатизмом высоких порядков: интегрирующие звенья вносят фазовый сдвиг по -90 каждое. Поэтому уже при втором порядке астатизма возникают проблемы с устойчи­востью системы. В связи с этим появляется необходимость вводить в систему дополнительные, так называемые корректирующие звенья. Тем не менее системы с порядком астатизма выше второго практически не используются. Однако не следует отчаиваться: уничтожение в формуле (6.13) даже первых двух слагаемых очень сильно уменьшает ошибку регулирования, так как эти слагаемые самые мощные и именно они вносят основной вклад в формирование ошибки регулирования.