6. 4. Выводы
1. Ошибка регулирования зависит как от формы управляющего сигнала, так и порядка астатизма системы.
2. Чем более динамичный входной сигнал, тем больший порядок астатизма требуется для сведения ошибки к нулю.
3. Для получения нулевой ошибки регулирования порядок астатизма должен быть на единицу больше числа ненулевых производных входного сигнала х(t).
4. Если порядок астатизма равен числу ненулевых производных функции x(t), то ошибка будет постоянной.
5. Если порядок астатизма меньше числа ненулевых производных входного сигнала, то ошибка регулирования будет возрастать со временем и может превысить допустимое значение.
6. Даже при очень динамичных входных сигналах х(t) есть смысл использовать астатические системы хотя бы первого порядка, ибо они исключают из состава ошибки самые мощные компоненты.
7. Увеличение коэффициента усиления системы, увеличивая коэффициент А0, уменьшает ошибку регулирования (см. (6.15)).
6. 5. Задачи для решения в аудитории
Задача 6.1. Передаточная функция ошибки от регулирующего воздействия:
T1>T3
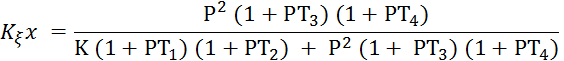
T2>T4
ξ (t) = const (отрицательная). Найти x (t).
Задача 6.2. Входная функция системы: x(t) = - At + Bt2
Передаточная функция замкнутой системы:
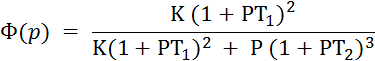
ξ (t) = ?
Задача 6. 3. Входной сигнал х(t) = Ае-αt . Передаточная функция разомкнутой системы
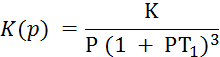
Какова ошибка регулирования ξ (t)? Учитывать только первые четыре члена ряда (6.13).
Тема 7. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ
Идея гармонической линеаризации нашла свое место в теории автоматического регулирования прежде всего потому, что имеется группа приближенных методов анализа нелинейных систем, основанных на принципе гармонического баланса. Они используются главным образом для исследования устойчивости нелинейных систем, а также устойчивости автоколебаний в этих системах.
При гармонической линеаризации нелинейного элемента считается что на его вход подается гармонический сигнал. При этом естественно ожидать, что на выходе нелинейного эвена сигнал будет негармоническим и в его составе будут высшие гармоники, общее количество которых теоретически может быть равно бесконечности. Тогда и в автоматической системе
в целом будут присутствовать эти гармоники, так как система замкнута и сигнал с выхода нелинейного звена рано или поздно, пройдя через группу других звеньев, попадет на его вход. Чтобы этот сигнал можно было считать гармоническим, необходимо, чтобы линейная часть системы обладала свойствами фильтра нижних частот и отфильтровывала все верхние гармоники, оставляя на входе нелинейного звена только первую. Если линейная часть нелинейной системы не обладает свойствами фильтра нижних частот, то использовать метод гармонической линеаризации нельзя, так как возникнут большие погрешности в анализе процессов, происходящих в системе.
Суть гармонической линеаризации сводится к замене нелинейного звена некоторым линейным эквивалентом по первой гармонике выходного сигнала. При этом вводится понятие коэффициента передачи линеаризованного звена по первой гармонике
![]()
где Vвх - амплитуда гармонического сигнала на входе звена; V1 вых - амплитуда первой гармоники сигнала на выходе звена.
Таким образом, гармоники более высоких порядков просто не учитываются. Поскольку звено все же нелинейное, естественно, что коэффициент Кн1 не будет постоянным при изменении амплитуды Vвх, так как форма искаженного негармонического сигнала на выходе звена при изменении амплитуды входного воздействия будет меняться. Например, на рис. 7.1, а показана простейшая нелинейность "насыщение". Если амплитуда Vвх будет в пределах от 0 до а, то звено фактически будет линейным и его коэффициент передачи:
![]()
На рис. 7.1, а обозначены по осям х1 и х2 – вход и выход нелинейного эвена.
Если же амплитуда сигнала на входе превысит уровень а, то в
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.