Коды, применяемые для канального кодирования

     Итак, в предыдущих пунктах мы рассмотрели экономное кодирование, направленное на уменьшение избыточности.

     При помехоустойчивом кодировании избыточность вводится в сообщение (в кодовую комбинацию) целенаправленно. Это делается с целью увеличения вероятности передачи т.е. уменьшения вероятности ошибки.

     В канале с достаточно большой вероятностью может произойти ошибка (в телеграмме одна буква превращается в другую). Чтобы повысить вероятность передачи можно каждую букву, например,  передавать трижды. То есть мы, заведомо увеличиваем избыточность. Но при этом скорость передачи уменьшится втрое.

     Пусть вероятность ошибки ещё больше, тогда нужно ещё больше повторять букву. Вследствие этого можно предположить, что чем больше уровень помех в канале, тем больше избыточности, то есть помехи , а скорость . Однако в действительности это далеко не так. Об этом говорится в теореме Шеннона:«Если производительность источника  меньше пропускной способности канала , то существует по крайней мере одна процедура кодирования/декодирования, при которой вероятность ошибочного декодирования и надежность могут быть сколь угодно малы. Если , то такой процедуры не существует». Следовательно в нашем примере с повторением букв, можно добиться сколь угодно верности и скорость передачи не будет равна нулю.   К сожаленью, эта теорема не указывает практических путей построения соответствующих кодов.

     В настоящее время известно множество кодов, которые с большим или меньшим успехом применяются для канального кодирования. Рассмотрим самые простые коды:

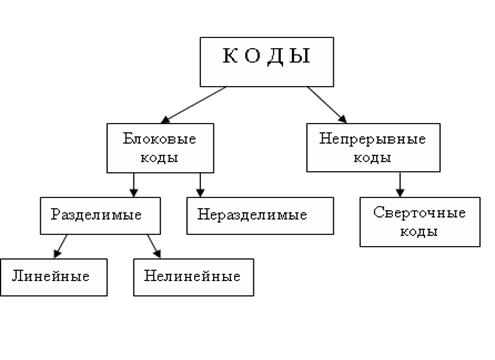
     Блочный код: Кодируются независимо блоки информационных символов одинаковой длины.

     При непрерывном кодировании кодируется первый символ, второй и т.д. Это похоже на то как формируется отклик (свертка). Он так и называется – сверточный код.

     Блоковые являются равномерными кодами. Делятся на разделимые и неразделимые. Если в кодовой комбинации блочного кода можно выделить информационные и проверочные символы, то код называется разделимым. Неразделимый код (код Рида Малера), это ни что иное, как функции Уолша. Они являются ортогональными.

     Для линейных кодов характерно свойство: линейная комбинация разрешенных кодовых слов является разрешенным кодовым словом.

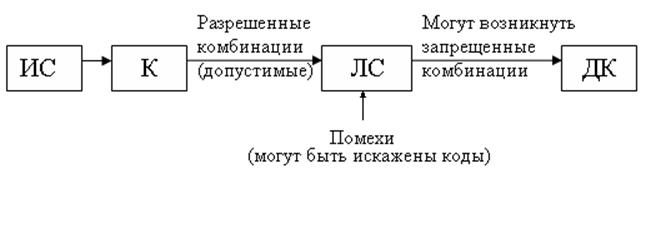
     Декодер разбивает все множество на классы. Разрешенных кодовых комбинаций всегда меньше чем всех передаваемых комбинаций.

    -код, , . К примеру, если код двоичный:  - комбинаций,  - разрешенных Явно избыточность.

     Задача декодеров разделить на 16 классов. А расстояние измеряется метрикой Хемминга.

,

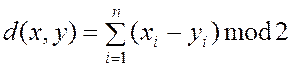где ,  - двоичные кодовые вектора.