Определение сигнала восьмизначным равномерным кодом (10110101). Линейные инвариантные к сдвигу цепи

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Кафедра теоретических основ радиотехники

Расчетно-графическое задание №1

по курсу «Теория электрической связи»

Факультет: РЭФ

Группа: РТВ14-91

Студент: Архипенко А. В.

Преподаватель: Тонконогов Е. А.

Новосибирск 2011

1.Сигналы и их характеристики

1.1.  Сигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту , где символ «0» соответствует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 1 мкс.

Вариант	Подвариант
	9
6	10110101

1.2. Требуется:

1.2.1. Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график

Функция Хевисайда имеет общий вид:

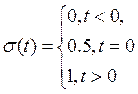
Для данного сигнала линейная комбинация функций Хевисайда:

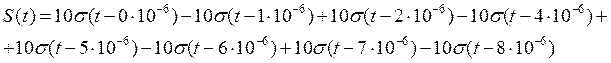
Временной график будет иметь вид:

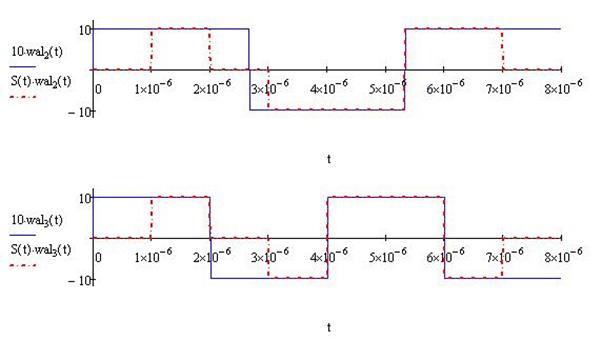
1.2.2. Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму

Функции Уолша определяются при помощи рекуррентного соотношения:

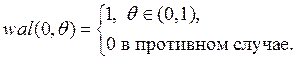
где 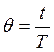- нормированное время. 

Для построения данного сигнала в базисе функции Уолша воспользуемся функцией

Wal_i(t) - функция Уолша i-ого порядка. i изменяется от 0 до 7.

Нормированные спектральные коэффициенты С_i, представляющие собой проекции сигнала S(t) относительно базиса Уолша:

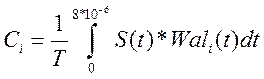
где  - исходный сигнал, - i-ая функция Уолша.

В итоге cпектральная диаграмма разложения исходного сигнала в базисе Уолша будет иметь вид:

1.2.3. Найти спектральную плотность сигнала относительно ядра Фурье, построить графики её модуля и аргумента

Для перехода описания сигнала во времени  к описанию в частотной области применим  прямое преобразование Фурье:

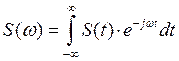
Для прямоугольного сигнала (симметричного относительно отсчёта времени  с длительностью  и амплитудой А) значение спектральной плотности:

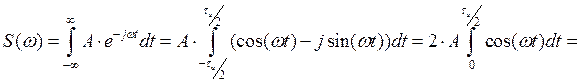
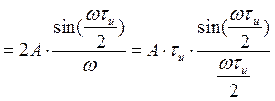
Данный сигнал S(t) представляет собой последовательность из двух одиночных прямоугольных видеоимпульсов смещенных во времени.

Спектральная плотность смещенного прямоугольного импульса определяется по свойству преобразования Фурье, называемого теоремой сдвига:

где  - задержка импульса

Определим длительность и задержку каждого из составляющих заданного сигнала

Длительность: с, с.

Задержка: с,  с.

Таким образом, получаем функцию спектральной плотности для данного сигнала:

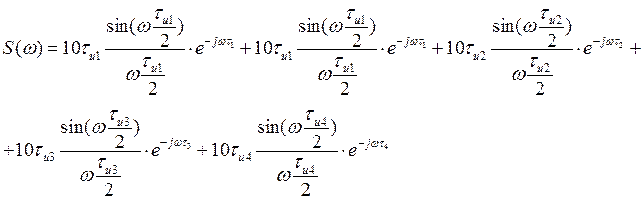
График модуля спектральной плотности:

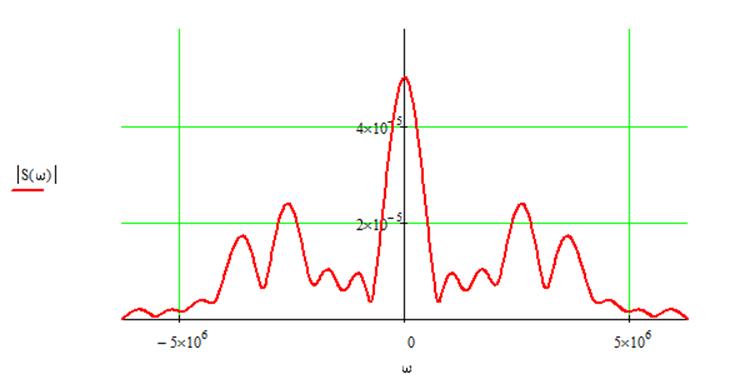
График аргумента спектральной плотности:

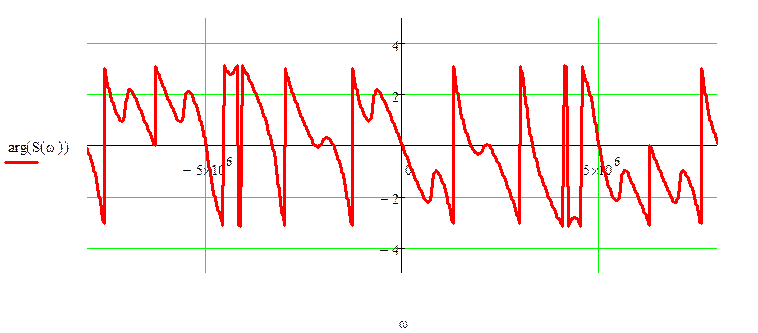
1.2.4. Найти спектр периодической последовательности, полученной повторением  данного сигнала, относительно комплексного базиса Фурье, построить амплитудную и фазовую спектральные диаграммы

Спектральная плотность связана соотношением с комплексными амплитудами периодического сигнала 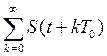, полученного повторением с периодом   одиночного импульса .

                                     ,                                  

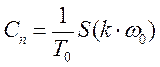
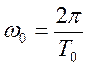
где ,

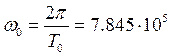Данное соотношение позволяет перейти от сплошного спектра одиночного импульса к дискретному спектру периодической последовательности импульсов.

Для наглядности графики амплитудныx и фазовыx спектральных диаграмм изобразим совместно с модулем и аргументом спектральной плотности сигнала соответственно:

Амплитудная спектральная диаграмма:

Фазовая спектральная диаграмма:

1.2.5. Найти автокорреляционную функцию сигнала, построить график

Для количественного определения степени отличия сигнала S(t) и его смещенной во времени копии S(t – τ) принято вводить автокорреляционную функцию (АКФ) сигнала S(t), равную скалярному произведению сигнала и копии:

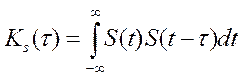
Свойства АКФ, необходимые для её построения:

1.   Автокорреляционная функция достигает максимума при =0 и равна при этом значению аргумента энергии сигнала:

                                                                         

2. Автокорреляционная функция обладает свойством сопряженной симметрии:

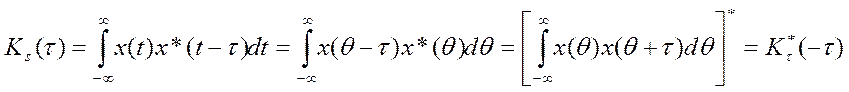 В частности, АКФ вещественного сигнала – четная функция.

Рассмотрим графически принцип определения АКФ. Для этого покажем степень связи (корреляции) сигнала  со своей копией, сдвинутой на величину  по оси времени. На представленных графиках  можно наблюдать оригинал и смещенную на величину копию сигнала.:

Значение АКФ при каждом n будет определяться как площадь пересечения оригинала и его сдвинутой копии. Значение АКФ между двумя соседними значениями n будет изменяться линейно. При отрицательных смещениях АКФ примет те же значения по свойству симметрии.