Определение сигнала восьмизначным равномерным кодом (10110101). Линейные инвариантные к сдвигу цепи, страница 2

График автокорреляционной функции заданного сигнала:

1.2.6. Определить эффективную ширину спектра

Полная энергия одиночного импульса может быть вычислена либо во временной области, либо в частотной  в соответствии с равенством Парсеваля:

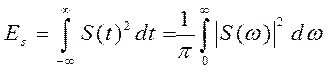
Эффективную ширину спектра определяем в частотной области. Находим частотный интервал, на котором сосредоточена основная часть энергии сигнала (90%-95%). Для этого изобразим график функции :

Глядя на график, видно, что основная энергия сигнала сосредоточена в частотном интервале приблизительно равном рад/с.

Тогда эффективную ширину спектра можно определить по формуле:

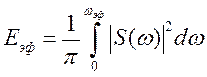
Таким образом, Дж

В данном случае берётся лишь положительная область спектра, но в силу симметричности для всей области спектра эффективная ширина его умножается на два:

Дж.

1.2.7. Найти сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ (частота среза  фильтра в МГц и крутизна  ФЧХ в рад/МГц приведены в таблице), построить временной график полученного сигнала.

Вариант	6
fср, МГц	2,5
Подвариант	0
S, рад/МГц	0,85

Передаточная функция цепи:

где- функция включения Хевисайда.

Исходный сигнал:

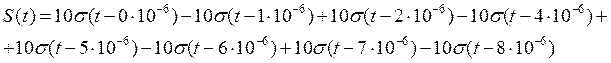
Представим исходный сигнал в операторном виде, применив прямое преобразование Лапласа:

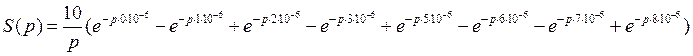
Заменив  на , получаем выражение для входного сигнала в частотной области:

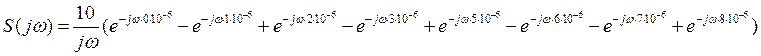
Спектральная плотность выходного сигнала есть произведение спектральной плотности входного (заданного) сигнала и передаточной функции:

Чтобы перейти к временной области сигнала, необходимо к спектральной плотности выходного сигнала применить обратное преобразование Фурье:

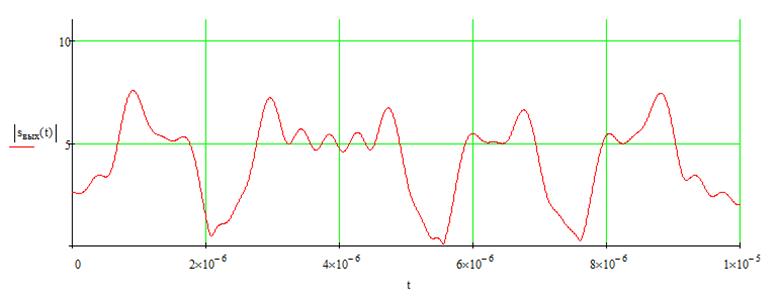
График выходного сигнала:

1.2.8. Найти сигнал, который получается из заданного при воздействии RC-фильтра НЧ с параметрами, указанными в таблице ( в кОм,  в мФ), построить временной график полученного сигнала

Вариант	6
R, кОм	2,5
Подвариант	0
C, мФ	0,95

Применим к исходному сигналу в операторном виде прямое преобразование Лапласа:

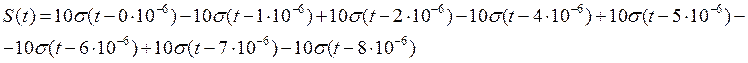
Передаточная функция фильтра в операторном ви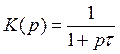де:

,    где с – постоянная времени

Выражение для выходного сигнала получаем как произведение передаточной функции фильтра и входного сигнала  в операторном виде:

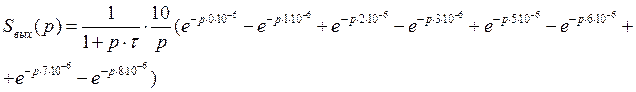
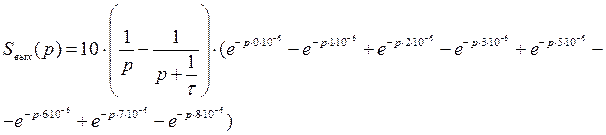
Сигнал на выходе можно представить как разность двух составляющих, одна из которых есть входной сигнал. Найдем обратное преобразование Лапласа от обеих составляющих:

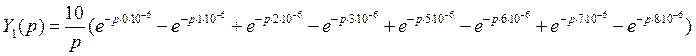
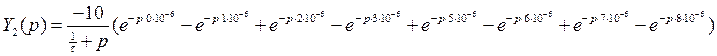
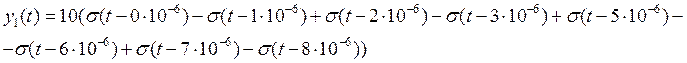
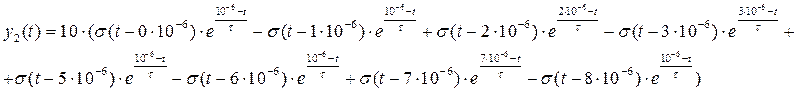
Откуда  

График выходного сигнала имеет вид:

2. Линейные инвариантные к сдвигу цепи

2.1. ЛИС-цепь определяется схемой согласно варианту, ее параметры ( в кОм,  в мкФ,  в мГн ) – согласно подварианту.

6

Подвариант	0
R1,кОм	3,0
R2,кОм	3,1
С1,мкФ	0,95
С2,мкФ	0,33
L1,мГн	2,0
L2,мГн	1,1

R₃=R₁

2.2. Требуется:

2.2.1. Найти комплексную частотную характеристику цепи, построить графики АЧХ и ФЧХ

Рассчитаем, опираясь на схему:

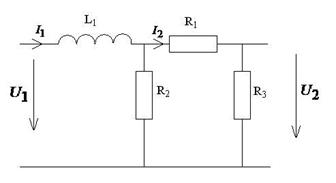
Комплексная частотная характеристика определяется по формуле:

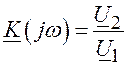
Т.к. выходные зажимы разомкнуты, найдём напряжение на выходе:

По методу делителя токов определим :

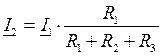
Следовательно:

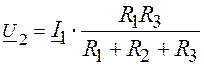
Свернём цепь относительно входного напряжения   для его определения через  и

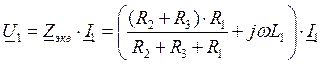
Получаем выражение для КЧХ:

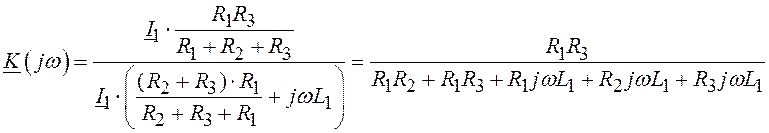
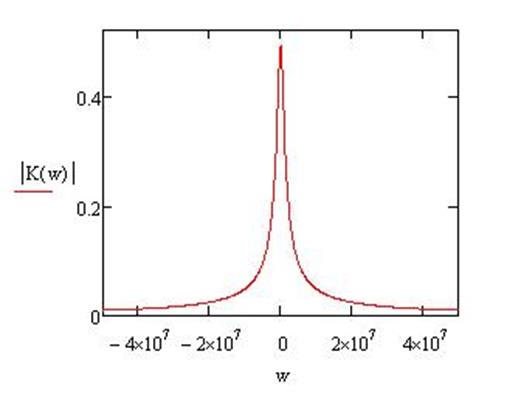
Амплитудно-частотная характеристика цепи:

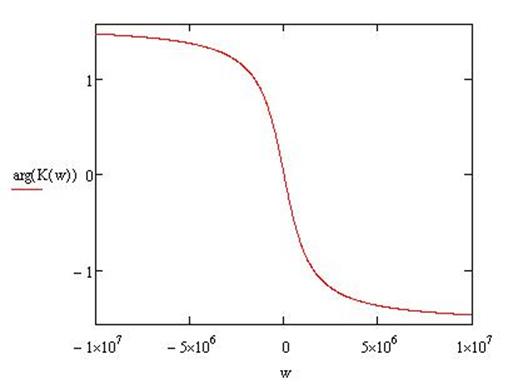
Фазо-частотная характеристика цепи:

2.2.2. Найти импульсную и переходную характеристики, построить графики

Импульсной характеристикой цепи называется функция  ,  представляющая собой отклик ЛИС-цепи на "бесконечно короткий импульс" (-функцию).

Импульсная характеристика связана с комплексной частотной характеристикой цепи  через обратное преобразование Фурье:

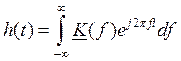
Учитываем, что импульсная характеристика удовлетворяет условию каузальности (причинности):

 при

График импульсной характеристики для данной цепи:

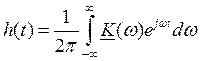
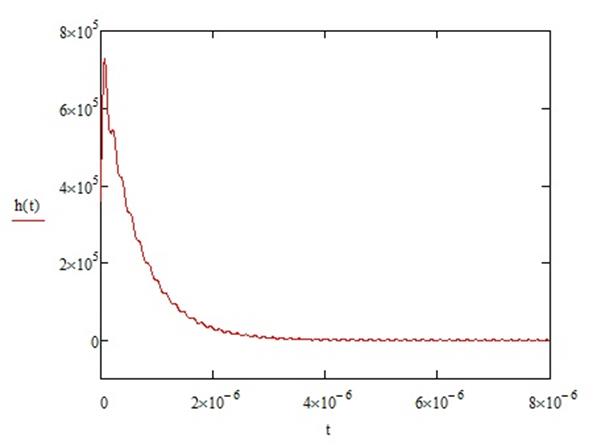
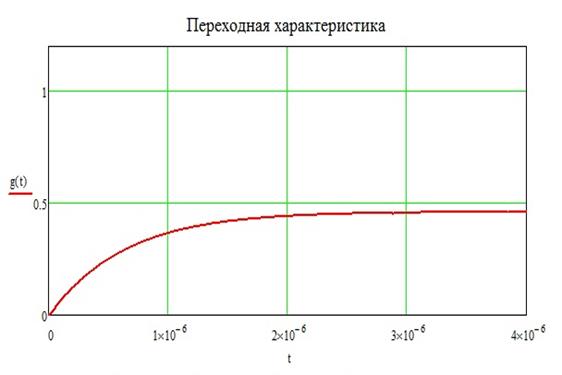
Переходная характеристика  представляет собою отклик цепи на функцию включения. Переходная характеристика выражается через импульсную характеристику следующим образом:

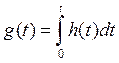
2.2.3. Найти отклик цепи на заданный сигнал, построить график

Запишем входной сигнал в виде интегрального выражения относительно ядра  :

                                                                   

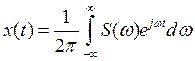
Это выражение представляет  "сплошной" суммой базисных функций  с 

" амплитудными коэффициентами" .

Следовательно, отклик ЛИС-цепи с КЧХ  на этот сигнал представляется интегралом:

                                                   

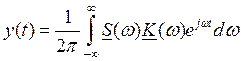
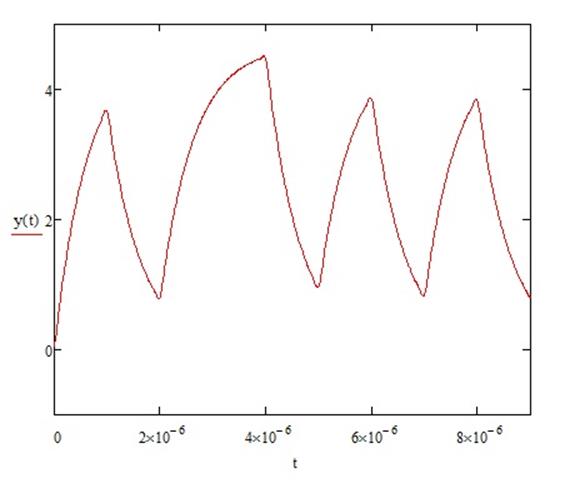
График отклика на заданный сигнал: