Определение сигнала восьмизначным равномерным кодом (11101001). Расчет ЛИС-цепи

1.  Сигналы и их характеристики

1.1.  Сигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту (табл. 1), где символ «0» соответствует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 1 мкс.

1.2.  Требуется:

·  Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график

·  Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму

·  Найти спектральную плотность сигнала относительно ядра Фурье, построить графики её модуля и аргумента

·  Найти спектр периодической последовательности, полученной повторением  данного сигнала, относительно комплексного базиса Фурье, построить амплитудную и фазовую спектральные диаграммы

·  Найти автокорреляционную функцию сигнала, построить график

·  Определить эффективную ширину спектра

·  Найти сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ (частота среза  фильтра в МГц и крутизна  ФЧХ в рад/МГц приведены в табл. 2), построить временной график полученного сигнала

·  Найти сигнал, который получается из заданного при воздействии RC-фильтра НЧ с параметрами, указанными в табл. 3 ( в кОм,  в мФ), построить временной график полученного сигнала

2.  Линейные инвариантные к сдвигу цепи

2.1.  ЛИС-цепь определяется схемой согласно варианту (табл. 4), ее параметры ( в кОм,  в мкФ,  в мГн ) – согласно подварианту (табл. 5).

2.2.  Требуется:

·  Найти комплексную частотную характеристику цепи, построить графики АЧХ и ФЧХ

·  Найти импульсную и переходную характеристики, построить графики

·  Найти отклик цепи на заданный сигнал, построить график

1.Сигналы и их характеристики

1.1.  Сигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту (табл. 1), где символ «0» соответствеует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 0.1 мкс.

                                                               Таблица 1

Вариант	Подвариант
	2
9	11101001

    1.2.   Требуется:

●   Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график.

Функция включения Хевисайда (рис.1) определяется выражением: 

                    

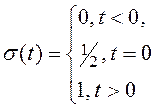
                                                                                  Рис.1.1. Функция включения Хевисайда

Математическая модель сигнала, представляющая собой линейную комбинацию функций включения, имеет следующий вид:

Временной график сигнала:

Рис.1.2. Временной график сигнала

·  Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму

Построим графики сигнала умноженного на соответствующую функцию Уолша:

График сигнала умноженного на нулевую функцию Уолша представляет собой сам сигнал.

Коэффициенты Уолша рассчитаем по формуле (помножим на  для нормирования коэффициентов):

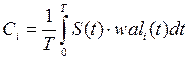
Подробно распишем вычисление первого коэффициента (т.к. остальные рассчитываются аналогично):

Ниже представлены функции Уолша, график сигнала умноженный на соответствующую функцию Уолша (друг под другом) и соответствующий коэффициент Уолша:

Рис1. Первая функция Уолша и график сигнала умноженного на первую функцию Уолша

Рис2. Вторая функция Уолша и график сигнала умноженного на вторую функцию Уолша

Рис3. Третья функция Уолша и график сигнала умноженного на третью функцию Уолша

Рис4.Четвертая функция Уолша и график сигнала умноженного на четвертую функцию Уолша

Рис5.Пятая функция Уолша и график сигнала умноженного на пятую функцию Уолша

Рис6.Шестая функция Уолша и график сигнала умноженного на шестую функцию Уолша

Рис7.Седьмая функция Уолша и график сигнала умноженного на седьмую функцию Уолша

По полученным коэффициентам построим спектральную диаграмму (отложим на ординат коэффициенты Уолша):

Спектральная диаграмма

·  Найти спектральную плотность сигнала относительно ядра Фурье, построить графики её модуля и аргумента