Разработка системы связи для передачи дискретных сообщений (код для сокращения избыточности источника – Хаффмена)

некогерентный), обработка сигнала в согласованном фильтре и помехоустойчивое (канальное) кодирование (код Хемминга).

     В зависимости об информации, известной о сигнале, различают когерентный приём (известна начальная фаза и частота радиоимпульса) и некогерентныйприём (начальная фаза и частота радиоимпульса неизвестны).

     В процессе передачи сигнал искажается помехами, при этом в приёмнике могут приниматься ошибочные решения:

 - при передачи элемента «0», принято решение о том, что передан элемент «1» - ошибка 1 рода; условная вероятность такого события обозначается Р₀₁.

 - при передачи элемента «1», принято решение о том, что передан элемент «0» - ошибка 1 рода; условная вероятность такого события обозначается Р₁₀.

   Формула (6.1) превращается в:

(6.2)

     В соответствии с этим появляются гипотезы: Н₀ – в линии только шум и Н₁ – в линии сумма сигнала и шума.

7. Расчёт характеристик системы согласно заданию 3.

7.1. Когерентный приём.

7.1.1. Расчёт порога для принятия решения.

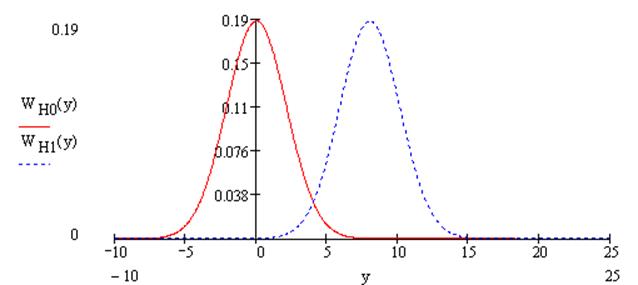
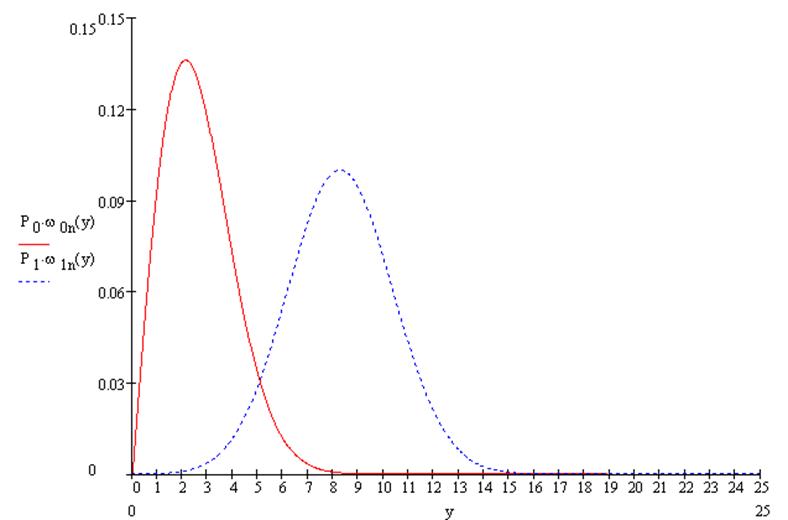
     Если в линии только шум с нулевым средним (гипотеза Н₀), то на выходе канала связи есть сигнал с Гауссовой плотностью распределения огибающей (см. рис. ***):

(7.1)

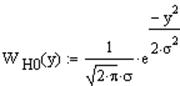
     Если в линии сумма сигнала и шума (гипотеза Н₁), то на выходе канала связи есть сигнал  с Гауссовой плотностью распределения огибающей (см. рис. 6):

(7.2)

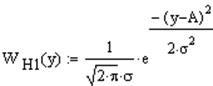
     Приравнивая (7.1) к (7.2) и учтя вероятности двоичных символов, найденные в пункте 5.2, запишем выражение для нахождения порога для принятия решений по критерию идеального наблюдателя:

(7.3)

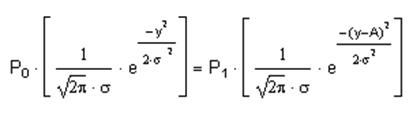
Отсюда получаем:  у_п = 3.947 В.

7.1.2. Расчёт средней вероятности ошибки.

Отношение правдоподобия – это отношение плотности распределения огибающей суммы сигнала и шума к плотности распределения огибающей шума, по значению которого можно принять решение о том, какой элемент передавался. С учётом того, что вероятности двоичных символов не равны, оно записывается так:

(7.4)

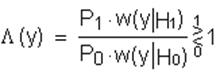
Вероятность ошибки 1 рода при когерентном приёме вычисляется интегрированием условной плотности распределения огибающей шума в пределах от у_п до бесконечности

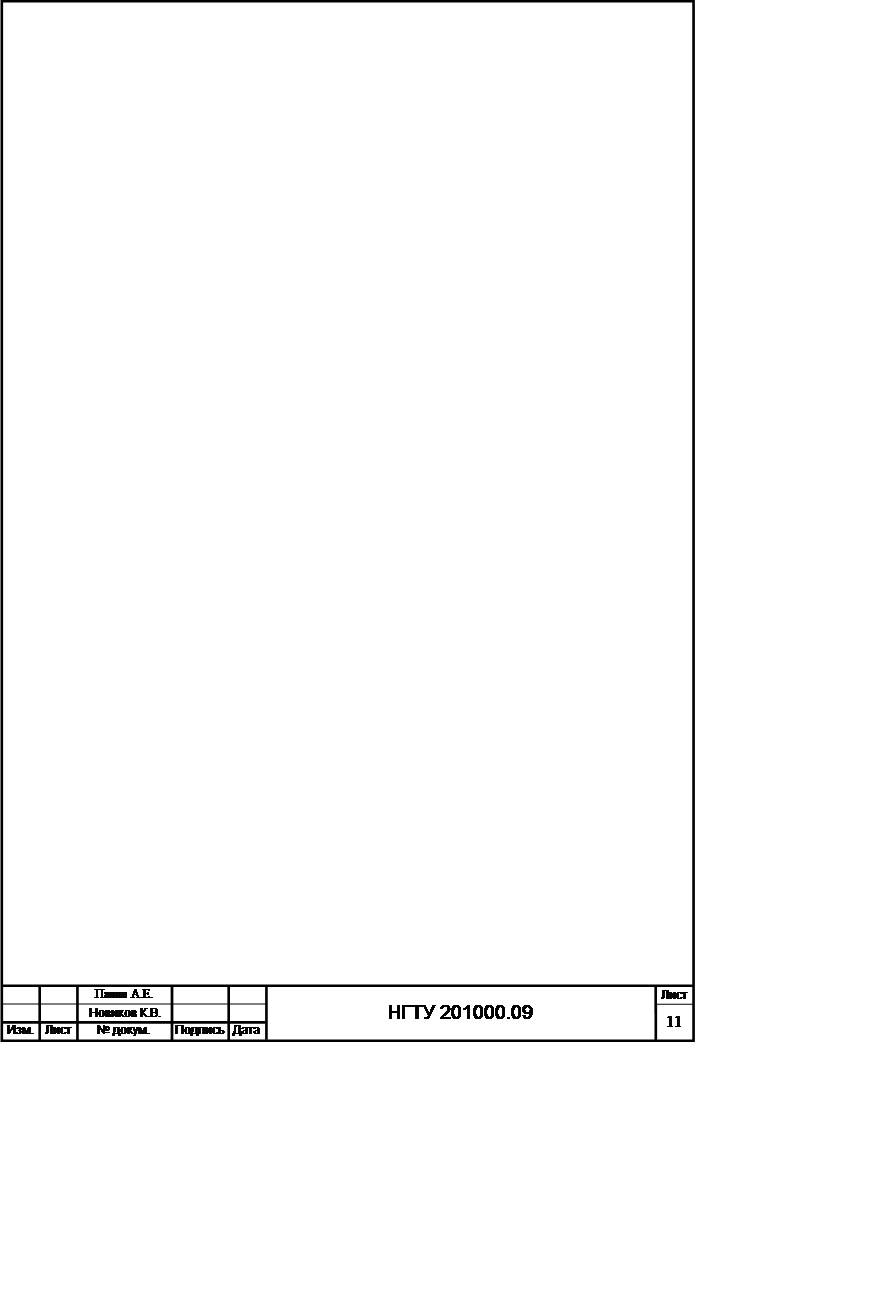Вероятность ошибки 2 родапри когерентном приёме вычисляется интегрированием условной плотности распределения огибающей суммы сигнала и шума  в пределах от минус бесконечности до у_п:       

(7.5)

Отсюда получаем: Р₁₀ = 0.028 и Р₀₁ = 0.031

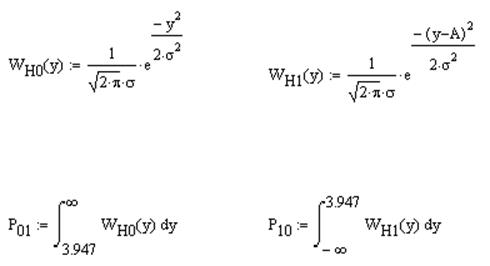
     Теперь по (6.2) и найденным в пункте (5.2) вероятностям двоичных символов кода, находим среднюю вероятность ошибки для когерентного приёма:

7.2. Некогерентный приём.

7.2.1. Расчёт порога для принятия решения.

     Если в линии только шум с нулевым средним (гипотеза Н₀), то на выходе канала связи есть сигнал с законом распределения Рэлея:

(7.6)

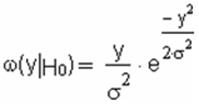
     Если в линии сумма сигнала и шума (гипотеза Н₁), то на её выходе есть сигнал  с обобщённым законом распределения Рэлея :

(7.7)

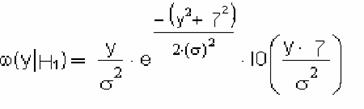
     где IO – модифицированная функция Бесселя.

     Приравнивая (7.6) к (7.7) и учтя вероятности двоичных символов, найденные в пункте (5.2), запишем выражение для нахождения порога для принятия решений по критерию идеального наблюдателя:

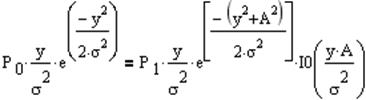
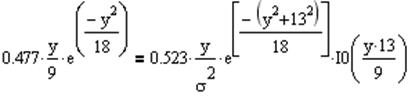
Отсюда получаем:  у_п = 5.075 В.

                              7.2.2. Расчёт средней вероятности ошибки.

        Вероятность ошибки 1 рода при некогерентном приёме вычисляется интегрированием условной плотности распределения огибающей шума  в пределах от у_п до бесконечности

        Вероятность ошибки 2 рода при некогерентном приёме вычисляется интегрированием условной плотности распределения огибающей суммы сигнала и шума  в пределах от минус бесконечности до у_п:        

(7.16)

(7.15)

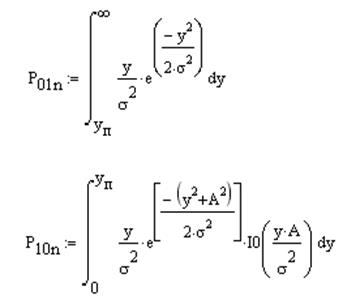
Отсюда получаем:

     Теперь по (6.2) и найденным в пункте 5.2 вероятностям двоичных символов кода, находим среднюю вероятность ошибки для некогерентного приёма:

7.2.3. Расчёт скорости передачи информации в канале с помехами.

     Расчётные формулы для некогерентного приёма такие