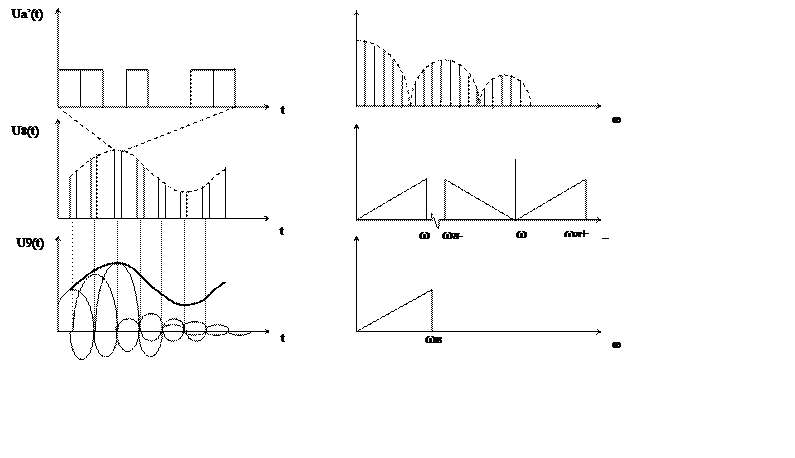
предназначен для преобразования электрического сигнала в исходное сообщение. Преобразование сообщения и сигналов в системе связи проиллюстрируем приведение временных и спектральных диаграмм на выходе каждого блока системы связи.
Временные и спектральные диаграммы.
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
 |
||||||||
|
|
|
||||||
|
|
V2
Vср(t)
Структурная схема когерентного приёма сигналов ОФМ.
Принцип работы:
Когерентный метод приёма (схема сравнения полярностей) заключается в том, что приёмный сигнал сначала детектируется, а затем поступает в схему сравнения. При этом сравниваются полярности посылок, полученных на выходе ФД (фазового детектора). Для сравнения полярностей посылок используется цепь задержки и сравнивающее устройство (СУ), на выходе которого образуется положительное напряжение, или предыдущая и настоящая посылка имеют одинаковую полярность, и отрицательное напряжение, когда полярности соседних посылок различны. В рассматриваемой схеме гетеродин (Г) синхронизируется по фазе с принимаемым сигналом при помощи системы синхронизации. Здесь фаза колебаний гетеродина также не однозначна и имеет два устойчивых состояния: «00» и «1800».
3.3 Принятие решения приёмником по одному отсчёту.
Сообщения передаются последовательностью двоичных символов «0» и «1», которые появляются с априорными вероятностями P(1)=0,54 и P(0)=0,46 соответственно. Этим символам соответствуют канальные сигналы S1(t) и S 2(t), которые точно известны в месте приёма . В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией s2=13,133 мкВт. Приёмник, оптимальный по критерию идеального наблюдателя, принимает решение по одному отсчёту смеси сигнала и помехи Z(t0)=Si(t0)+x(t0) на интервале элемента сигнала длительности Т. Плотность распределения вероятности в точке Z(t0):
W(X/S1)=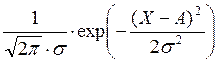
=
=
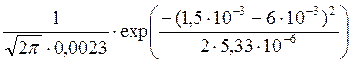=25,95
W(X/S2)=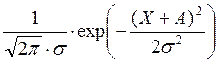
=
=
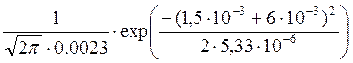=0,886
Пороговое отношение правдоподобия:
l0=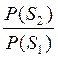
=
=0.85
Функция отношения правдоподобия:
lx=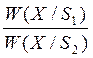
=
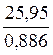=29,286
Т.к. l0<lx (0.85 < 29,286), то приёмник выдаёт S1. Таким образом, приёмник зарегистрирует символ «1».
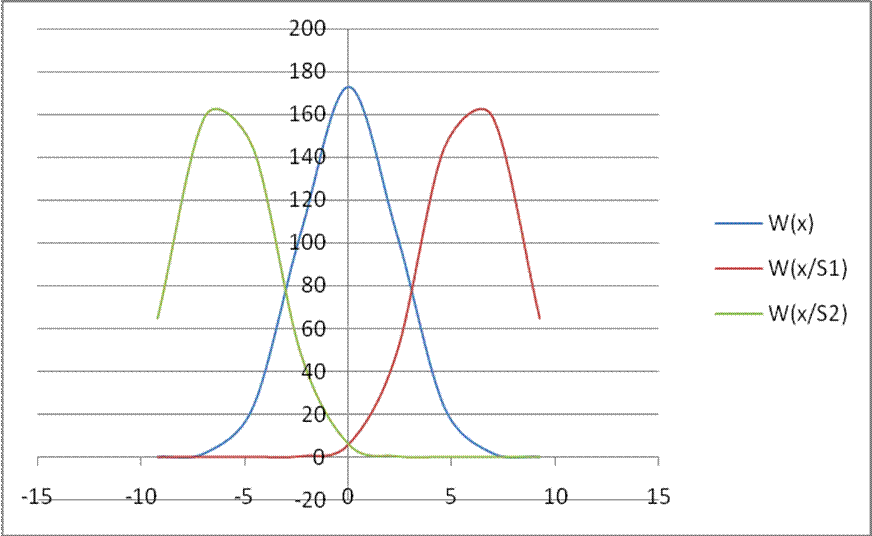
Приведём таблицу для построения графиков плотности распределения условных вероятностей.
Таблица 1.
|
x,мВ |
-9,233 |
-6,9247 |
-4,6165 |
-2,3082 |
0 |
2,3082 |
4,6165 |
6,9247 |
9,233 |
|
W(x) |
0,058 |
1,92 |
23,3905 |
104,8288 |
172,8335 |
104,8288 |
23,3905 |
1,92 |
0,0580 |
|
W(x/S1) |
0 |
0 |
0,0044 |
0,2657 |
5,8941 |
48,1021 |
144,4167 |
159,5056 |
64,8097 |
|
W(x/S2) |
64,8097 |
159,5056 |
144,4167 |
48,1021 |
5,8941 |
0,2657 |
0,0044 |
0 |
0 |
3.4 Вероятность ошибки на приёмнике.
Рассчитаем вероятность неправильного приёма двоичного сигнала и среднюю вероятность в рассматриваемом приёмнике для заданного вида сигнала (ОФМ) и способа приёма (ССП(кг)).
При расчётах полагаем, что полоса пропускания реального приёмника определяется шириной спектра двоичных сигналов ОФМ и определяется по формуле
пр офм=
=2*V=2*30000=60
кГц; Т – длительность элемента сигнала.
Pош
офм кг=1-Ф(
h);
h=
=
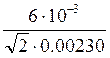=1.84
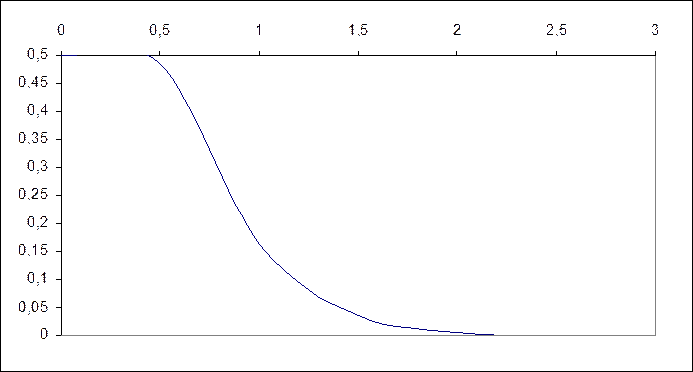
Значение вероятности ошибки определяем по таблице
значений функции V(x)=1-Ф(h)
Pош
офм кг=1-Ф(1.84*)= 0.07186
Таблица 2.
|
h |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
|
0 |
0.707 |
1.41 |
2.121 |
2.83 |
3.535 |
|
Pош |
0,50000 |
0,484 |
0,16152 |
0,03572 |
0,00511 |
0,000466 |
3.5 Выигрыш в отношении сигнал/шум при применении оптимального приёмника.
В предположении оптимального приёма (фильтрации) сигнала, определим:
А) Максимально возможное отношение сигнал/шум 
=
=
=
;
-
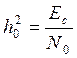
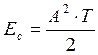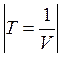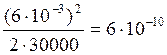энергия сигнала, 
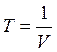- длительность элемента сигнала,
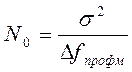- спектральная
мощность помехи,
, 
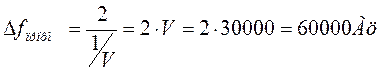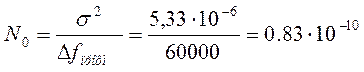, следовательно 
, 
.
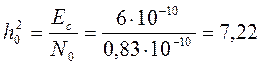Б) Выигрыш в отношении сигнал/шум при оптимальном приёме по сравнению с рассматриваемым приёмником.
При оптимальном приёме форма сигнала на выходе не
сохраняется (т.к. приём узкополосный). Максимальное отношение сигнала к помехе
(в точке 
) обеспечивается потому, что характеристика
K(
) является
неравномерной (K- коэффициент передачи).
Применяют сигналы большой длительности.
В схеме неоптимального приёмника после синхронного
детектора нет интегратора, который есть в оптимальном приемнике. До синхронных
детекторов стоят фильтры (приёмнике Котельникова фильтров нет). Оптимальные
фильтры дают на выходе максимальную помехоустойчивость: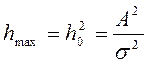
,
.
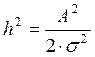
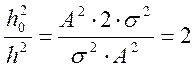Вывод: Выигрыш в отношении сигнал/шум при оптимальном приёме по сравнению с рассматриваемым приёмником равен двум.
3.6 Максимально возможная помехоустойчивость при заданном виде сигнала.
Для определения максимально – возможной помехоустойчивости приёма определим среднюю вероятность ошибки при оптимальном приёме для ОФМ кг.
Из результатов видно, что вероятность ошибки при оптимальном приёме резко уменьшилась.
3.7 Принятие решения приёмником по трём независимым отсчётам.
Определим, какой сигнал будет зарегистрирован на приёме при условии, что решение о переданном сигнале принимается по совокупности трёх независимых отсчётов на длительности элемента сигнала Т, имеющие следующие значения:
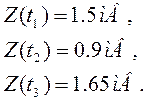
А=6 мВ.
Для принятия решения воспользуемся отношением правдоподобия, сравнив его с пороговым отношением:
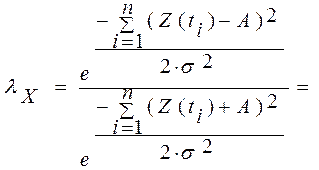
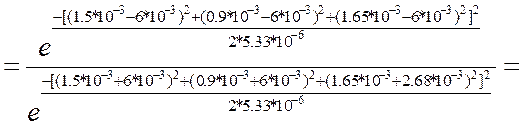1.0020771371937;
известно, 
= 0,85.
Тогда 
(0.85 < 1.0020771371937), в итоге на
выходе получим сигнал S1, т.е.
«1».
3.8 Возможность ошибки при использовании метода синхронного накопления.
Определим ожидаемую, в данном случае, среднюю вероятность ошибки, считая, что в приёмнике используется метод синхронного накопления(n – число отсчётов).
Считаем, что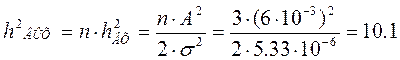 
,
отсюда 
;
.
В методе синхронного накопления амплитуда возрастает. Помеха в разных сигналах имеет разные фазы. Помеха возрастает по мощности в n раз, однако, сигнал лучше накапливается. За счёт этого повышается помехоустойчивость приёма.
3.9 Расчёт шума квантования при передаче сигналов методом ИКМ.
Определим мощность шума квантования:
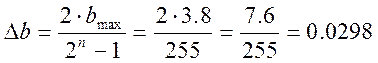
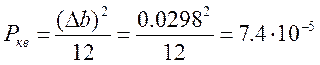
Отношение мощности сигнала к мощности
шума 
при максимальной амплитуде аналогового
сигнала.
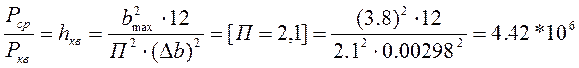
3.10 Приём c использованием согласованного фильтра.
Считаем, что символы «1» и «0» передаются сложными сигналами S1(t) S2(t), которые представляют собой последовательности прямоугольных импульсов положительной и отрицательной полярности длительности Т. Приём этих сигналов осуществляется с помощью согласованного фильтра.
Дана дискретная последовательность из одиннадцати элементов:
1-1-1-1 1-1 -1 1 -1 1 1.
Для этой последовательности нарисуем структурную схему приёмника с оптимальным фильтром, осуществляющего синхронный приём сообщений.
|
|
|
|
|
1 -1 -1 -1
1
-1 -1 1
-1
1 1
Вход
 |
 |
 |
 |
 |
 |
 |
 |
||||||||||
 |
|||||||||||||||||
К Выход
|
Uп
Схема 3.
При синхронном приёме сообщений ключ К замыкается в области, когда передаваемая дискретная последовательность совпадает с последовательностью, на которую рассчитан фильтр. Поэтому на выходе максимальный сигнал, равный амплитуде, но противоположный по полярности. Значит для достижения помехоустойчивости Uп=0.
Структурная схема приёмника с оптимальным фильтром, осуществляющего синхронный приём сообщений:
Cхема 4
|
|
|
1 -1
-1 -1 1 -1
-1
1 -1 1 1
|
|
Вход
 |
|||||||||||||
 |
 |
|
|||||||||||
|
|
|
|||||||||||
Выход
 |
При асинхронном приёме ключа нет, но в решающем устройстве выбираются 2 порога Uп1 и Uп2.
3.11 Форма сигналов при передаче символов «1» и «0».
Изобразим форму сложного сигнала при передаче по каналу связи символа «1», ему соответствует последовательность из 11 элементов:
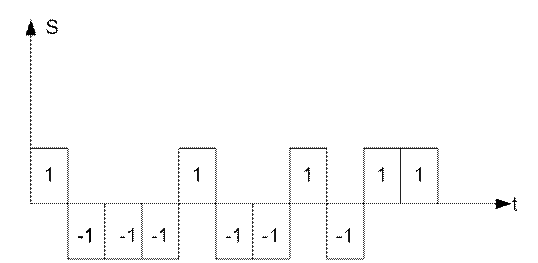
рисунок 1.
Изобразим форму сложного сигнала при передаче по каналу связи символа «0»:
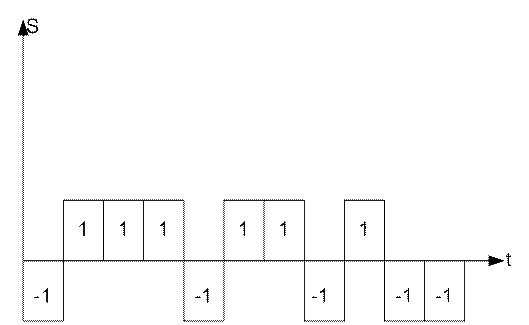
рисунок 2.
3.12 Импульсная характеристика согласованного фильтра.
Импульсной характеристикой согласованного фильтра называется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
