Расчет воздействия заданного сигнала и стационарного аддитивного шума на вход заданной ЛИС-цепи

Контрольное задание №2.

1.  Случайные процессы и их воздействие на ЛИС-цепи.

  На вход заданной ЛИС-цепи воздействуют заданный сигнал и стационарный аддитивный шум с нулевым математическим ожиданием и спектральной плотностью мощности (Вт/Гц).

   Требуется:

·  Найти отношение сигнал/шум(ОСШ) по напряжению и по мощности на входе цепи.

Для выполнения этого задания найдём значение дисперсии:

 соответственно математическое отклонение

  Откуда находим, что отношение сигнал/шум равен:

по напряжению

 по мощности.

·  Найти СПМ шума и ОСШ по напряжению и по мощности на выходе цепи.

Для выполнения этого задания вернёмся к РГЗ№1.

По найденой  ,  находим СПМ: , где .

В результате получаем график:

Найдём ОСШ по напряжению и по мощности:

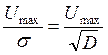,                           ,здесь  заменим т.к. при таком пороге дисперсия растёт не значительно (судя по графику). А значение  берём равным 3,5(из графика в РГЗ№1).

Получаем:                                            -ОСШ по напряжению.

ОСШ по мощности находим аналогично, возведя в квадрат числитель и знаменатель:

                      -ОСШ по мощности.

·  Найти эффективную ширину спектра и интервал корреляции шума на выходе цепи.

По графику находим максимальное значение

-+

      Эффективная ширина спектра:                                                

      Интервал корреляции шума:

·  Построить графики плотности распределения вероятности мгновенного значения шума и смеси сигнала с шумом на выходе цепи для момента времени, когда сигнал максимален.

Воспользуемся Гауссовым распределением вероятности:

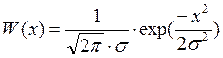 - для шума.

График имеет вид:

Найдём график плотности распределения вероятности мгновенного значения сигнала с шумом на выходе цепи для момента времени, когда сигнал максимален:

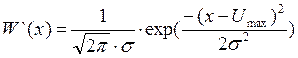  - смесь сигнала с шумом:

·  Определить вероятности событий, состоящих в том, что шумовое напряжение в некоторый момент времени превысит заданный порог  и в том, что смесь сигнала с шумом окажется ниже порога (момент времени должен соответствовать максимальному значению сигнала на выходе цепи).

Найдём вероятность события, состоящего в том, что шумовое напряжение в некоторый момент времени превысит заданный порог:

     Найдём вероятность события, состоящего в том, что смесь сигнала с шумом окажется ниже порога:

2.  Модулированные колебания.

  Несущее гармоническое колебание, имеющее амплитуду , частоту , и начальную фазу  модулируется по амплитуде гармоническим колебанием, имеющим частоту , амплитуду  и начальную фазу  

  2.2Требуется:

·  Найти спектр амплитудно-модулированного колебания.

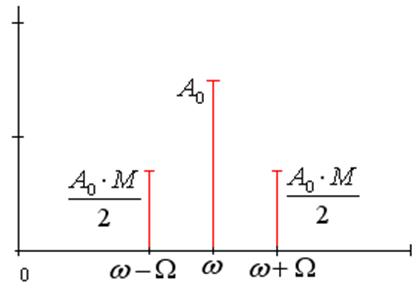
Спектр амплитудно-модулированного колебания состоит из трёх гармоник: несущей и двух боковых. Боковые отстают и опережают несущее на величину .

Следовательно спектр АМК имеет вид:

Здесь                              

·  Определить коэффициенты модуляции и мощности несущего колебания и боковых составляющих.

Коэффициент модуляции несущего колебания определяется как:

Коэффициент мощности несущего колебания:

Коэффициент боковых составляющих:

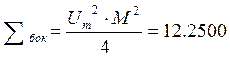
·  Рассчитать и изобразить временную и векторную диаграммы амплитудно-модулированного колебания.

Изобразим временную диаграмму АМК.

    АМК имеет аналитическое выражение:

    Изобразим временную диаграмму АМК:

  Изобразим векторную диаграмму АМК:

2.2 Гармоническое колебание, имеющее амплитуду Um,  частоту fo и начальную фазу

модулируется по частоте(фазе) гармоническим колебанием, имеющем частоту Fи начальную фазу (девиация частоты для ЧМ).

       Требуется:

·  Записать выражение модулированного колебания:

Анализ ЧМ- частот с математической точки зрения гораздо сложнее, чем исследование АМ- колебаний. Поэтому основное внимание уделяем простейшим однотональным сигналам.

 В случае однотонального ЧМ- сигнала мгновенная частота

                 На основании формулы

   полная фаза такого сигнала

 При частотной модуляции между величинами s(t) и

 имеется связь вида

где s(t)- сигнал, k- коэффициент пропорциональности.

Поэтому

Значит мгновенное значение ЧМ- сигнала

·  Найти спектр модулированного колебания, построить диаграмму.

Модель ЧМ- сигнала с любым значением индекса модуляции:

где Jk- функция Бесселя k- го индекса.

 График  функции Бесселя:

Чтобы построить диаграмму, определим

                           где

Спектральная диаграмма:

·  Определить практическую(эффективную) ширину спектра.

С ростом девиации частоты расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами k>m+1. отсюда следует оценка  практической (эффективной) ширины спектра:

    ЧМ- сигнал занимает полосу частот, приблизительно равную удвоенной девиации частоты.