Пояснительная записка
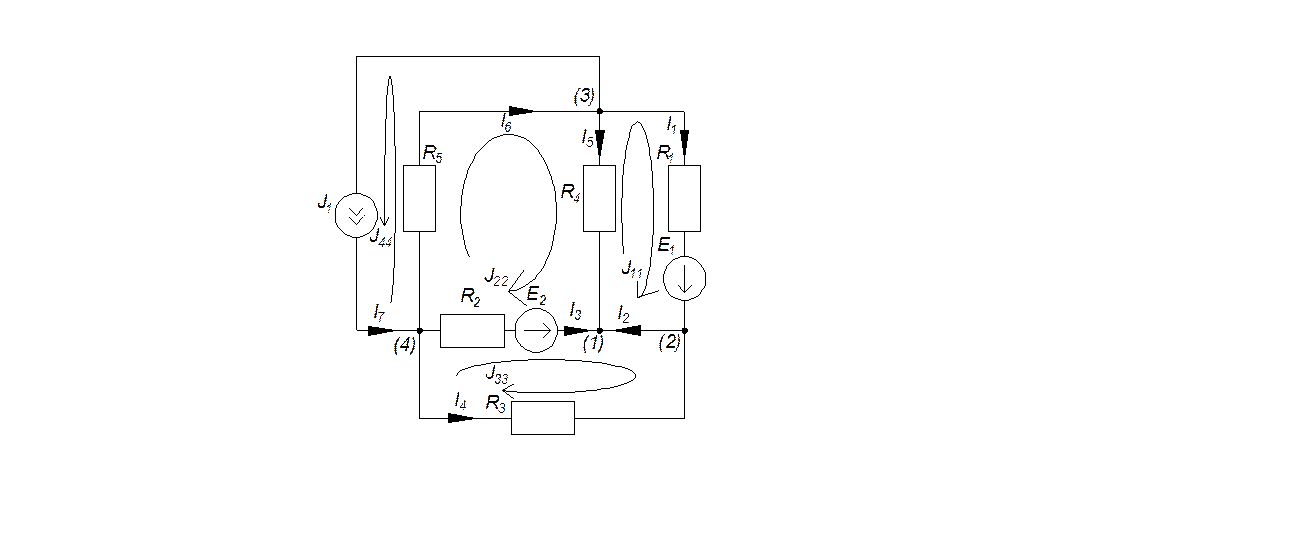 1.Метод контурных токов.
1.Метод контурных токов.
Рис. 1.1
Дано: R1=R2=R3=4(Ом); R4=R5=5(Ом); E1=50В; E2=60В; J1=10А; ϕ2=0В;
Выберем направления контурных токов (Рис. 1.1), контурный ток J44=J1, I7=J1, перенесем в правую часть, и запишем уравнения:
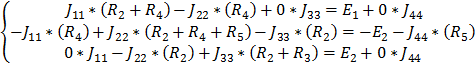 (1.1)
(1.1)
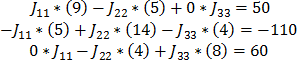
Решим эту систему из трех уравнений по методу Крамера:
Определитель матрицы коэффициентов:
|
|
![]()
![]()
Определители матриц со столбцами свободных членов:
|
|
![]()
![]()
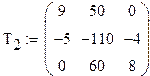
![]()
![]()
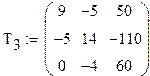
![]()
![]()
Разделим полученные определители на определитель матрицы коэффициентов, и найдем значения контурных токов:
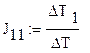
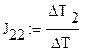
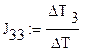 (1.2)
(1.2)
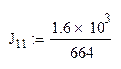
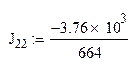
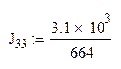
J11=2.41А J22=-5.663A J33=4.669A J44=10A
Опираясь на Рис. 1.1 найдем связь между контурными токами, и токами в ветвях:
![]()
![]()
![]()
![]()
![]()
![]() (1.3)
(1.3)
I1=2.41А
I2=2.41А- 4.669A =-2.259A
I3=4.669A+5.663A =10.331A
I4 = -4.669A
I5= -5.663A -2.41А=-8.072A
I6=-5.663A+10A=4.337A
2. 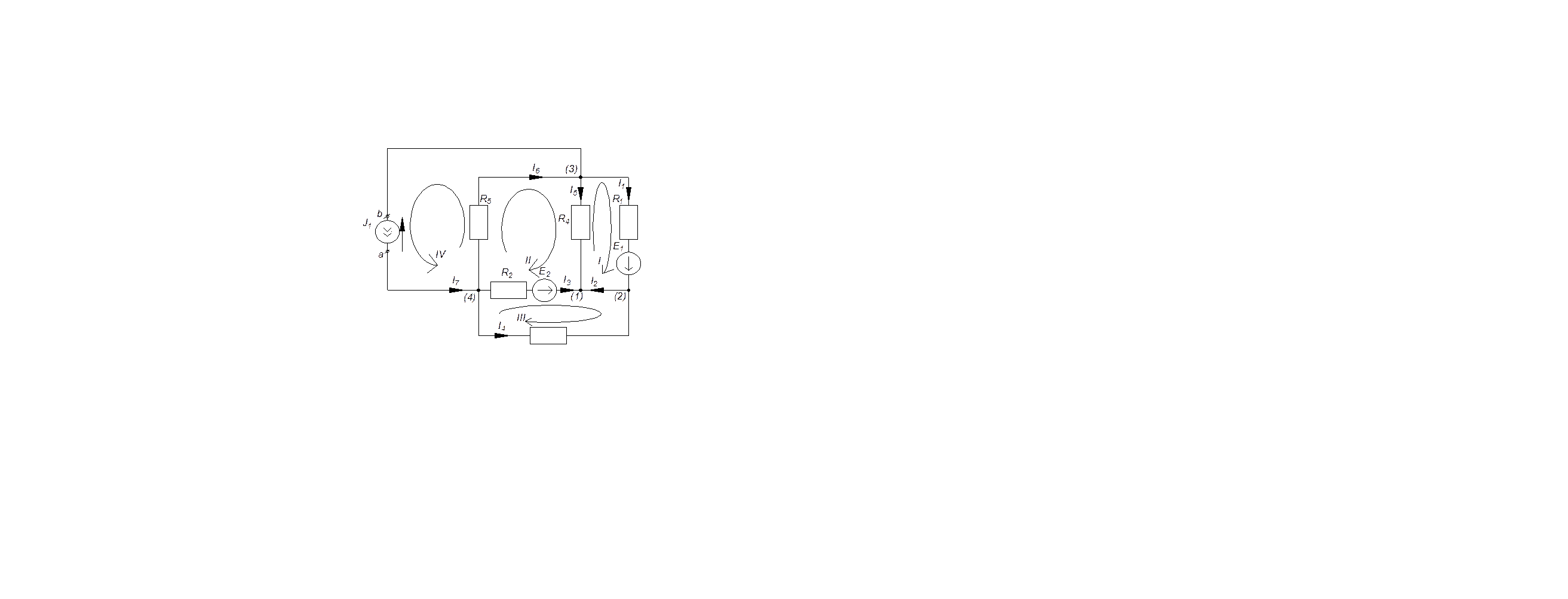 Проверка
по законам Кирхгофа и баланс мощностей
Проверка
по законам Кирхгофа и баланс мощностей
Рис. 2.1
Составим систему уравнений по законам Кирхгофа, включающую в себя три уравнения записанные по первому закону, три уравнения по второму закону:
(2)![]()
(1)![]()
(4)![]()
(I)![]()
(II)![]()
(III)![]() (2.1)
(2.1)
Подставим значения, чтобы убедится в правильности составления уравнений:
(2)-2.41А+4.669А-2.259А=0
(1)-10.331A+2.259A+8.072=0
(4)-10A+4.337A+10.331A-4.669A=0
(I)2.41A*4(Ом)+8.071А*5(Ом)-50В=0
(II)4.669А*4(Ом)+10.331А*4(Ом)-60В=0
(III)-8.072А*5(Ом)-10.331А*4(Ом)+4.337А*5(Ом)+60В=0
Запишем уравнения для потребляемой и генерируемой мощности:
Для нахождения потребляемой мощности возводим токи в квадрат, умножая на сопротивление ветви:
![]() (2.2)
(2.2)
Ppotr=2.412А*4(Ом)+10.3312А*4(Ом)+(-4.669)2А*4(Ом)+(-8.072)2А*5(Ом)+4.3372А*5(Ом)
Ppotr=957.229Вт
Для генерируемой мощности, алгебраическая сумма мощностей источников:
![]() (2.3)
(2.3)
Для того чтобы найти напряжение на ab воспользуемся вторым законом Кирхгофа (обойдем IV контур против часовой стрелки):
-Uab+I6*R5=0 (2.4)
![]()
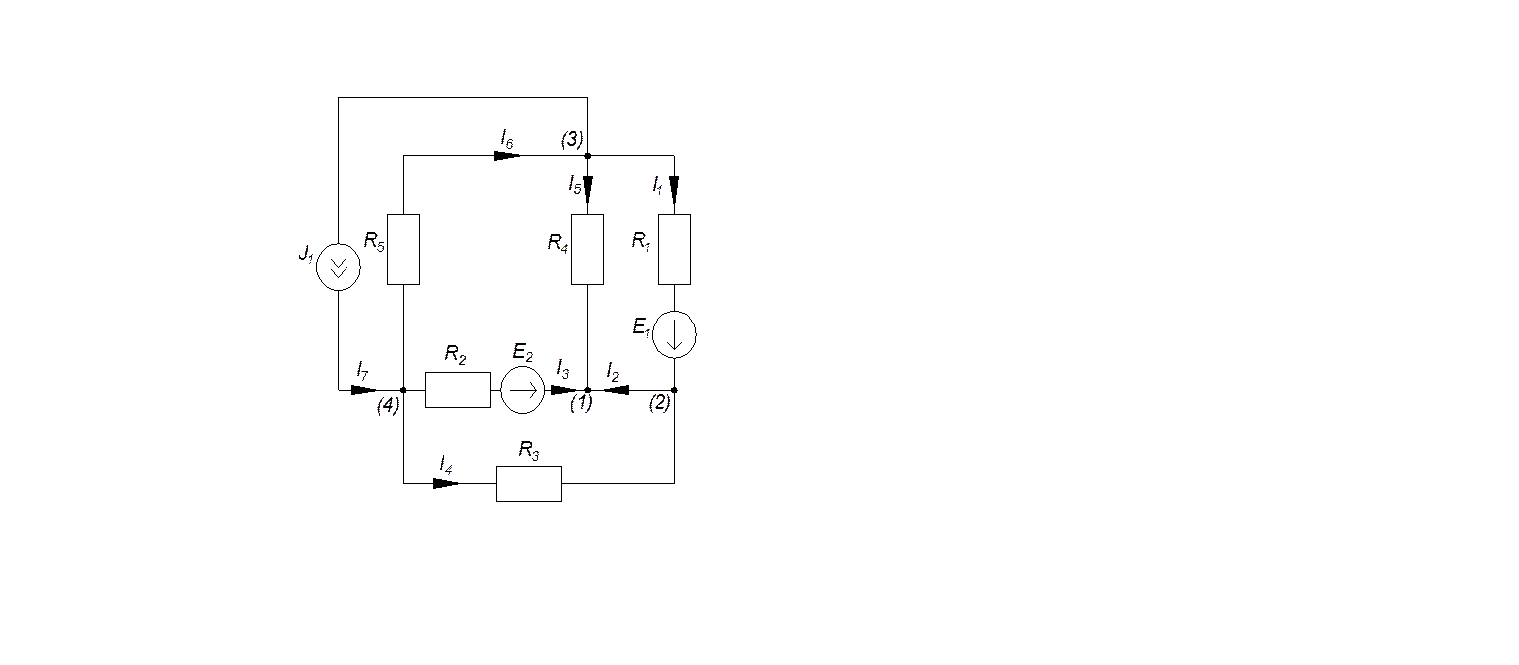 Uab=4.337A*5(Ом)
= 21.687В
Uab=4.337A*5(Ом)
= 21.687В
Pgen=50В*2.41А+60В*10.331А+10А*21.687В=957.229Вт
3. Метод узловых потенциалов
Рис 3.1
Из условия задачи, потенциал узла (2) считают равным нулю. Т.к. ветвь (2)-(1) не содержит элементов, потенциал узла (1) равен потенциалу узла (2)(ϕ1=0В).
Найдем потенциалы узлов (3) и (4) составив систему уравнений:
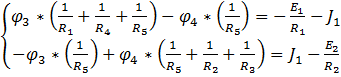 (3.1)
(3.1)
![]()
Воспользуемся методом Крамера:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
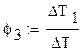
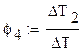 (3.2)
(3.2)
![]() = -40.361В
= -40.361В ![]() = -18.675В
= -18.675В
Так как искомый ток(I2) это ток закоротки, найти его можно только выразив из законов Кирхгофа.
Выразим его из первого закона Кирхгофа, записав уравнение для узла (2):
(2)![]() (3.3)
(3.3)
|
|
Найдем токи I1 и I4 по закону Ома(разность потенциалов плюс алгебраическая сумма ЭДС ветви, деленная на сопротивление ветви):
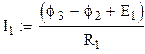 (3.4)
(3.4)
![]()
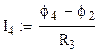 (3.5)
(3.5)
![]()
I2=![]()
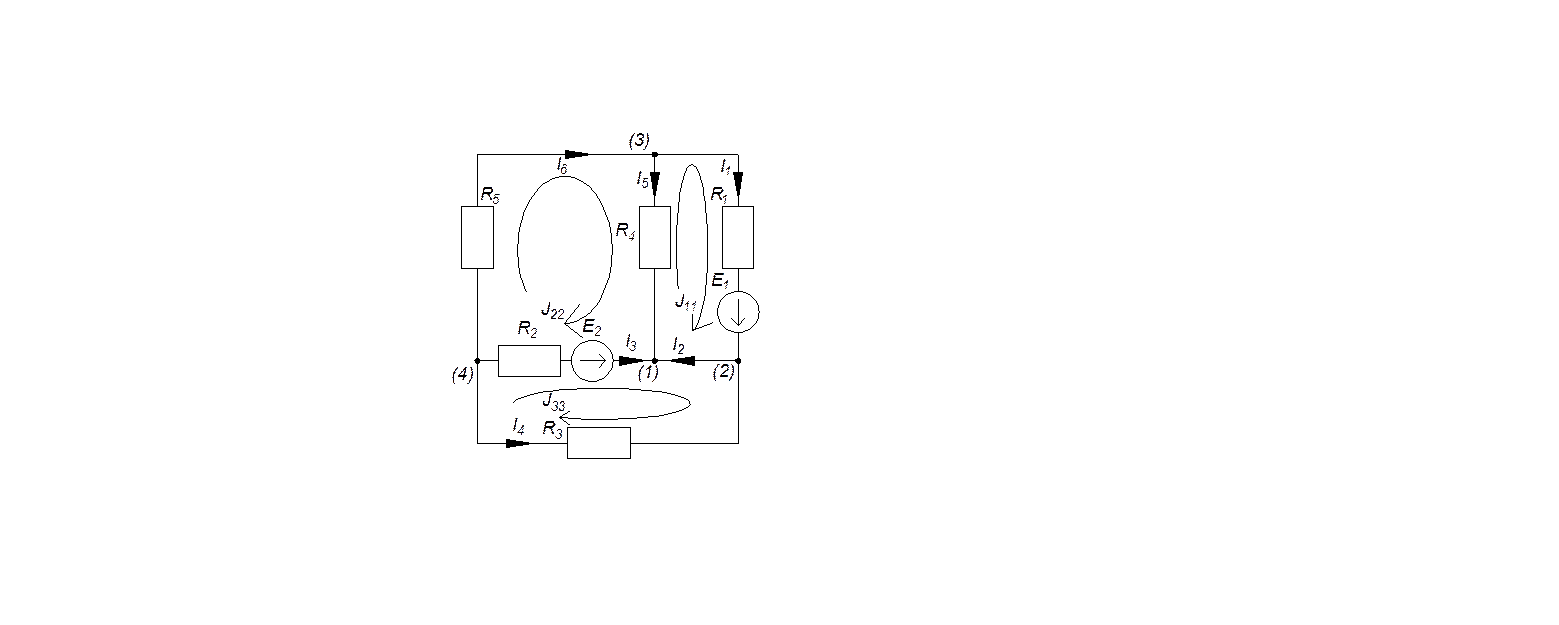 4.Метод наложения (суперпозиции)
4.Метод наложения (суперпозиции)
1) Частичный ток от источников ЭДС.
Для того чтобы посчитать частичный ток от источников ЭДС, заменим источник тока на его внутреннее сопротивление (бесконечность), и посчитаем ток I3 по методу контурных токов.
Рис. 4.1
Составим систему из трех уравнений, и найдем три контурных тока:
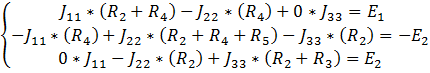 (4.1)
(4.1)
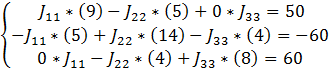
Воспользуемся методом Крамера:
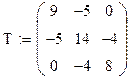
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.