Случайные процессы и их воздействие на ЛИС-цепи. Модулированные колебания

Определить вероятности событий, состоящих в том, что шумовое напряжение в некоторый момент времени превысит заданный порог  (см. табл. 6) и в том, что смесь сигнала с шумом окажется ниже порога.

 Вероятность события, состоящего в том, что шумовое напряжение в некоторый момент времени превысит заданный порог:

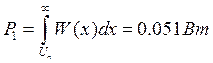
Соответственно, вероятность события, состоящего в том, что смесь сигнала с шумом окажется ниже порога:

4. Модулированные колебания

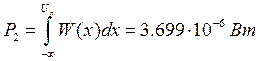
 4.1. Несущее гармоническое колебание, имеющее амплитуду  (В), частоту  (МГц), и начальную фазу  (рад) модулируется по амплитуде гармоническим колебанием, имеющим частоту , амплитуду и начальную фазу  (все параметры определяются табл.).

Подвариант	3
	6
	0,9

Вариант	0
	15
	0,65

·  Найти спектр амплитудно-модулированного колебания

Амплитудная модуляция заключается в изменении амплитуды несущего гармонического колебания:

в соответствии с изменениями первичного сигнала. Для простоты анализа примем, что первичный сигнал представляет собой гармоническое колебание низкой (в сравнении с частотой несущего колебания ) частоты Ω. Это случай тональной модуляции. Тогда амплитудно-модулированное колебание имеет вид:

где M – коэффициент модуляции

 

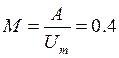
  Спектр – это совокупность коэффициентов, определяющих амплитуды гармонических колебаний, составляющих рассматриваемое колебание. Найти спектр – представить АМК в виде суммы гармонических колебаний и определить их амплитуды. Спектр амплитудно-модулированного колебания состоит из трёх гармоник: несущей и двух боковых. Боковые отстают и опережают несущее на величину .

Пусть  ,

Тогда, раскрывая скобки, получаем выражение:

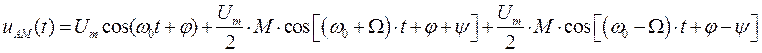
Запишем спектр:

                

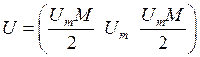
Амплитудная спектральная диаграмма АМ-колебания:

Фазовая  спектральная диаграмма АМ-колебания:

·  Определить коэффициент модуляции и мощности несущего колебания и боковых составляющих

Коэффициент модуляции был рассчитан в предыдущем пункте:

Мощность несущего колебания:

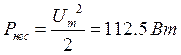
Суммарная средняя мощность боковых составляющих:

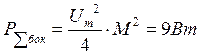
·  Рассчитать и изобразить временную и векторную диаграммы амплитудно-модулированного колебания

Для построения временной диаграммы воспользуемся формулой:

Для построения векторной диаграммы, принимают что комплексная плоскость вращается по часовой стрелке с угловой скоростью , тогда вектор несущего колебания длиной неподвижен, а векторы боковых колебаний вращаются в противоположных направлениях с одинаковыми угловыми скоростями  и , так что их сумма всегда лежит на линии, вдоль которой направлен вектор несущего колебания.

Запишем отдельно выражения для боковых и несущего колебаний:

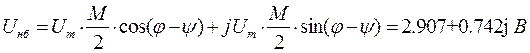
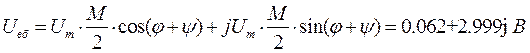
4.2  Гармоническое колебание, имеющее амплитуду , частоту , и начальную фазу  (табл. 7) модулируется по частоте (фазе) гармоническим колебанием, имеющим частоту  и начальную фазу  (девиация частоты  для ЧМ или индекс модуляции  для ФМ определяются подвариантом).

·  Записать выражение модулированного колебания

При угловой модуляции гармонического колебания результирующий сигнал имеет постоянную амплитуду и зависящую от первичного сигнала фазу, поэтому его можно записать в общем виде, как

где Ф(t) – фаза колебания, а  - его начальная фаза.

Частота модулируется по гармоническому закону:

Тогда фаза модулированного колебания:

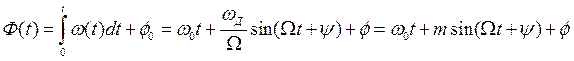
Индекс модуляции, численно равный при тональной модуляции:

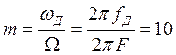
Тогда, выражение для угловой модуляции примет вид:

·  Найти спектр модулированного колебания, построить диаграмму

Запишем УМ-колебание в виде:

Известна формула:

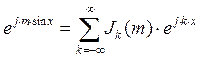
где  - функция Бесселя первого рода k-го порядка. С учетом этого равенства

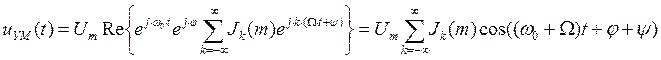
 Таким образом, даже при тональной модуляции спектр УМ-колебания имеет бесконечно много составляющих, амплитуды которых определяются значениями функции Бесселя , рассматриваемой как функция номера гармоники  при заданном значении