Разработка системы связи для передачи дискретных сообщений (способ передачи – амплитудная телеграфия с пассивной паузой)

Демодулятор выделяет огибающую ВЧ колебаний, пришедших с канала связи и, сравнивая уровень поступившего сигнала с пороговым, различает принятые сигналы. На выходе декодера получатель сообщений получает передаваемый сигнал b(t).

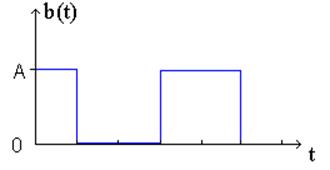
Рис. 5 Восстановленный сигнал.

4.2 Построение кода. Кодирование построенным кодом произвольной фразы длиной не менее 15 символов.

В данной работе рассматривается способ передачи информации амплитудной телеграфией с пассивной паузой, что соответствует принятию решения о том, что передавался символ «0» (сигнала нет) или символ «1» (сигнал есть). Чтобы можно было воспользоваться этим способом передачи, нужно закодировать символы комбинацией «нулей» и «единиц». Для этого воспользуемся код Хаффмана.

Процедура кодирования:

1.  Все символы алфавита записываются в порядке убывания вероятностей.

2.  два нижних символа соединяются скобкой, из них верхнему приписывается символ «1», нижнему «0».

3.  Вычисляется сумма вероятностей, соответствующих этим символам алфавита.

4.  все символы алфавита снова записываются в порядке убывания вероятностей, при этом только что рассмотренные символы «склеиваются», т.е. учитываются как единый символ с суммарной вероятностью.

5.  повторяются шаги 2,3 и 4 до тех пор, пока не останется ни одного символа алфавита, не охваченного скобкой.

Следуя вышеизложенной процедуре, получим:

Табл. 2 Кодовое дерево Хаффмана

Закодируем фразу: “ КЕДР ДЕРЖАВА МОРС”.

Код: 010 1111 110100 100  

        110100 1111 100 0111 1011 11011 1011                          

             1010 000 100 1100

При кодировании использовались две теоремы Шеннона и правило кодирования.

Теорема Шеннона (в отсутствии шума). Среднюю длину кодовых слов для передачи символов источника А при помощи кода с основанием m можно как угодно приблизить к величине Н / log(m).

Теорема Шеннона (в присутствии шума). Если производительность источника (Н^¢(А)) меньше пропускной способности канала С, то существует хотя бы одна процедура кодирования – декодирования, при которой вероятность ошибочного кодирования и ненадежность (Н(АêВ)) могут быть сколь угодно малы. Если Н^¢(А) > С, то такой процедуры не существует.

Правило кодирования. Если символы алфавита неравновероятны и не зависимы, то более  вероятным символам ставятся в соответствие более короткие кодовые комбинации.

5. Расчет характеристик системы связи согласно п. 1.2.1.

5.1 Источник.

Энтропия – среднее количество информации, приходящееся на один символ.

Энтропия источника:

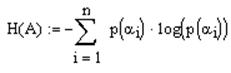
Максимальная энтропия источника (энтропия источника для равновероятных символов):

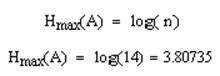
Избыточность источника:

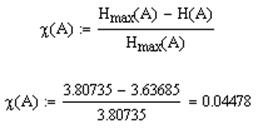
5.2 Код.

Средняя длина кодового слова (сумма произведений длины i-го элемента на вероятность i-го элемента):

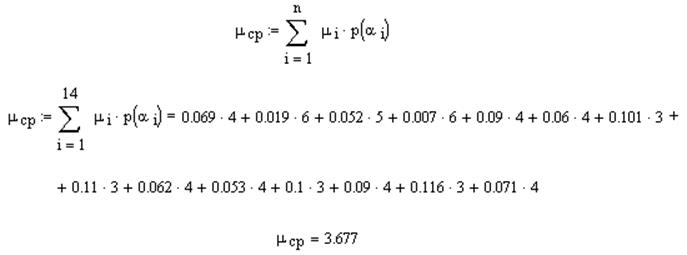
Априорные вероятности:

Вероятность передачи единицы:

Вероятность передачи нуля:

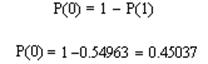
Энтропия кода:

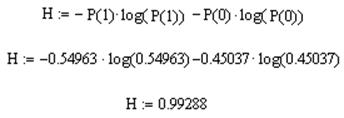
Максимальная энтропия кода:

Избыточность кода:

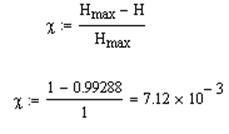
Скорость передачи информации:

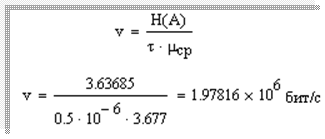
6. Описание процесса принятия приемником решения при приеме сигнала.

Модулированный сигнал u(t), проходя через канал связи, подвергается воздействию помехи. На выходе получаем сигнал z(t), который является смесью переданного сигнала с помехой.

Приемник в результате анализа принятой реализации смеси z(t) на интервале t должен установить, какой из возможных сигналов присутствует в наблюдаемом  процессе, и принять решение о приеме символа 1 или 0. Для различения сигналов в приемнике необходимо устанавливать начало и конец интервала анализа каждой реализации z(t). Эта задача решается устройством синхронизации (позволяет определять начало и  окончание каждого элемента сигнала). В  данной работе предполагается, что синхронизация идеальна, т.е. моменты   начала и  окончания  каждой посылки известны точно.

Но из-за помех приемник может дать ложный результат, и вместо передаваемого символа мы получим другой. Эти ошибки можно классифицировать:  

1.  Ошибка первого рода (ложная тревога): при передаче элемента 0 принято решение о том, что передан   элемент  1; условная вероятность такого события обозначается  P01.

2.  Ошибка второго рода (не обнаружение сигнала): при передаче элемента 1 принято решение о том, что передан   элемент  0; условная вероятность такого события обозначается  P10.

В данном задании помеха аддитивная и представляет собой  гауссовский