Определение сигнала восьмизначным равномерным кодом (11101001). Расчет ЛИС-цепи, страница 3

 

Тогда эффективную ширину спектра можно определить по формуле:

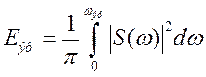
Подставляя в данный интеграл , находим, что эффективная ширина спектра:

В данном случае мы предполагали лишь положительную область спектра, но в силу симметричности для всей области спектра эффективная ширина его умножается на 2.

·  Найти сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ (частота среза  фильтра в МГц и крутизна  ФЧХ в рад/МГц приведены в табл. 2), построить временной график полученного сигнала

Таблица 2

Вариант	9
fср, МГц	2,8
Подвариант	2
S, рад/МГц	0,8

Передаточная функция цепи имеет вид:

где- функция включения Хевисайда.

Исходный сигнал, записанный как линейная комбинация функций включения:

Представим исходный сигнал в операторном виде, применив прямое преобразование Лапласа:

Заменив  на , получаем выражение для входного сигнала в частотной области:

Выражение для выходного сигнала в частотной области можно получить путем перемножения комплексной частотной характеристики цепи и входного сигнала.

    

Тогда выходной сигнал во временной области может быть получен как обратное преобразование Фурье от выходного сигнала в частотной области:

    

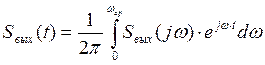
График выходного сигнала имеет вид:

График выходного сигнала

·  Найти сигнал, который получается из заданного при воздействии RC-фильтра НЧ с параметрами, указанными в табл. 3 ( в кОм,  в мФ), построить временной график полученного сигнала

                                     Таблица 3

Вариант	9
R, кОм	2,8
Подвариант	9
C, мФ	0,8

Представим исходный сигнал в операторном виде, применив прямое преобразование Лапласа:

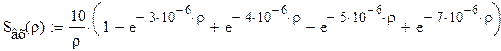
Передаточная функция фильтра в операторном виде:

    

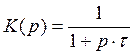
где - постоянная времени, которая определяется следующим образом:

Выражение для выходного сигнала можно получить путем перемножения передаточной функции фильтра и входного сигнала  в операторном виде:

Преобразуем выражение для :

Т.о. сигнал на выходе можно представить как разность двух составляющих, одна из которых есть входной сигнал. Найдем обратное преобразование Лапласа от обоих составляющих:

Откуда:

График выходного сигнала, построенный с помощью математического пакета MathCAD, имеет вид:

График выходного сигнала

2. Линейные инвариантные к сдвигу цепи

2.1ЛИС-цепь определяется схемой согласно варианту (табл. 4), ее параметры ( в кОм,  в пФ,  в мГн ) – согласно подварианту (табл. 5).

9

            Таблица 4Таблица 5

Подвариант	8
R1,кОм	2,2
R2,кОм	1,2
R3,кОм	1,7
С1,пФ	80

·             2.2     Требуется:  Найти комплексную частотную характеристику цепи, построить графики АЧХ и ФЧХ

КЧХ можно найти как отношение выходного напряжения к входному:

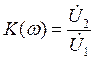
Для нахождения входного напряжения свернем схему относительно входных зажимов:

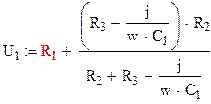Для нахождения выходного напряжения, воспользуемся методом делителя токов:

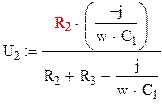Тогда КЧХ:

Построим графики АЧХ и ФЧХ комплексно частотной характеристики:

·  Найти импульсную и переходную характеристики, построить графики

Импульсная характеристика – отклик цепи на дельта функцию. В теории сигналов, КЧХ связана с импульсной характеристикой парой преобразований Фурье.

Импульсная характеристика цепи:

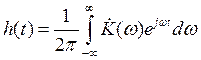
Построим график импульсной характеристики:

Переходная характеристика – интеграл от импульсной характеристики с переменным верхним пределом интегрирования:

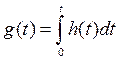
Построим график переходной характеристики:

·  Найти отклик цепи на заданный сигнал, построить график

В теории сигналов, отклик цепи может быть найден как обратное преобразование Фурье от произведения КЧХ на спектральную плотность сигнала:

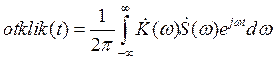
Построим график отклика цепи: