Определение сигнала восьмизначным равномерным кодом (11101001). Расчет ЛИС-цепи, страница 2

  Для перехода описания сигнала во времени  к описанию в частотной области  используют прямое преобразование Фурье:

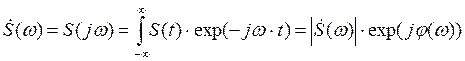
  Таким образом, одиночный импульс, заданный на всей бесконечной оси времени, имеет сплошной спектр в виде непрерывной функции частоты , которая называется спектральной плотностью.

Значение спектральной плотности прямоугольного импульса находится из формулы:

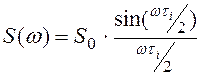
 Используем, одну из основных теорем о спектрах: теорему о спектре сигнала смещённого во времени :

 Найдём длительность и задержку исходного сигнала:

      

 Тогда выражение для спектральной плотности будет иметь вид:

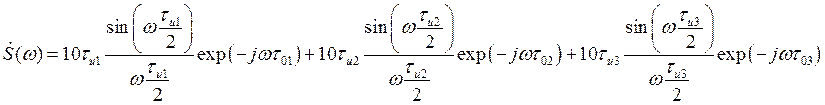Построим АЧХ и ФЧХ для функции спектральной плотности:

График модуля спектральной плотности сигнала

График аргумента спектральной плотности сигнала

·  Найти спектр периодической последовательности, полученной повторением  данного сигнала, относительно комплексного базиса Фурье, построить амплитудную и фазовую спектральные диаграммы

Рассмотрим непериодический сигнал конечной длительности . Спектральная  плотность  сигнала определяется выражением прямого преобразования Фурье:

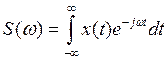
Повторение финитного сигнала  с периодом , большим, чем длительность , дает периодический сигнал 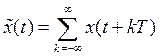, который в силу своей периодичности может быть представлен рядом Фурье со спектральными коэффициентами, определяемыми выражением:

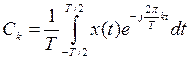
Сравнивая последние два равенства и учитывая, что интеграл в бесконечных пределах от финитной функции равен интегралу по интервалу, содержащему носитель функции, можно записать равенство:

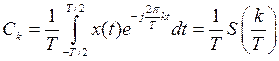
Таким образом, спектральная плотность импульсного сигнала имеет форму огибающей спектральных коэффициентов ряда Фурье периодической последовательности, образованной повторением данного импульсного сигнала с произвольным периодом. 

Коэффициенты ряда Фурье даже для вещественного сигнала в общем случае являются комплексными. Для удобства графического представления рассматривают отдельно модули и аргументы коэффициентов  , при этом совокупность  называется амплитудным спектром, а - фазовым спектром сигнала. Если сигнал  принимает вещественные значения, амплитудный спектр обладает свойством четности, а фазовый – свойством нечетности.

Для наглядности на графиках амплитудный и фазовый спектр совместим соответственно с модулем и аргументом спектральной плотности сигнала.

Амплитудный спектр сигнала

Фазовый спектр сигнала

·  Найти автокорреляционную функцию сигнала, построить график

Одной из важных временных характеристик детерминированных сигналов, устанавливающих энергетическую связь сигнала  с его сдвинутой на величину  копией , является автокорреляционная функция (АКФ). Для сигналов с ограниченной областью АКФ вычисляется по формуле:

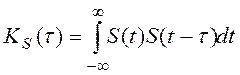
В теории сигналов также доказывается, что АКФ и энергетический спектр связаны парой преобразований Фурье:

Графически изобразим принцип метода определения АКФ. Для этого покажем степень связи (корреляции) сигнала  со своей копией, сдвинутой на величину  по оси времени. На данном графике можно наблюдать оригинал и копию сигнала без смещения. Затем будем смещать копию на величину  (пусть  )

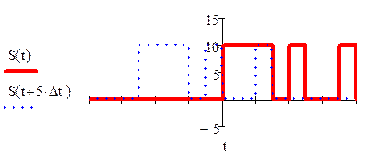
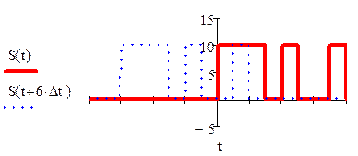
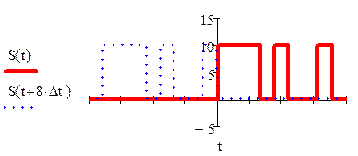На промежутках  АКФ равна нулю:

 

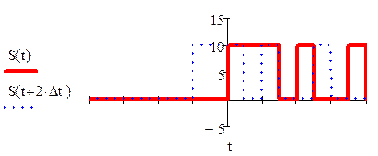
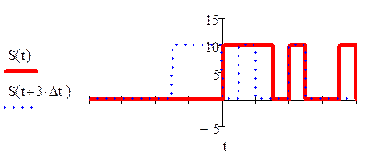
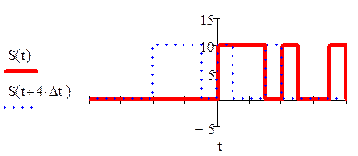
По данным графикам сигнала и его сдвинутой копии, легко построить АКФ. Для этого необходимо посчитать площадь пересечения сигнала и его сдвинутой копии. Ясно, что функция  достигнет своего максимума при , так как любой сигнал полностью коррелирован с самим собой. При этом максимальное значение корреляционной функции равно энергии сигнала. Точки для построения АКФ можно найти умозрительно, т.к. пересечения прямоугольного импульса с его сдвинутой копией представляется суммой определенных интегралов функции с амплитудой 10.

Построим график АКФ:

·  Определить эффективную ширину спектра

Энергия одиночного импульса может быть вычислена либо во временной области, либо в частотной в соответствии с равенством Парсеваля:

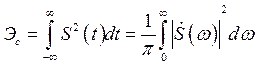
В частотной области можно определить эффективную ширину спектра сигнала. Это такой частотный интервал, в котором сосредоточена подавляющая часть полной энергии сигнала. Обычно 90% или 95%.

Эффективную ширину спектра определим по формуле:

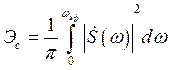
Для определения эффективной частоты  построим график квадрата модуля спектральной плотности сигнала:

График функции

Из графика видно, что основная часть энергии сигнала сосредоточена в частотном интервале . Где  - эффективная частота.