Силы, действующие на автомобиль. Радиусы эластичного колеса. Коэффициент общего дорожного сопротивления. Коэффициент сцепления. Тяговая характеристика авто. Анализ конструкции и расчет главной передачи, страница 3

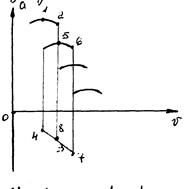
Рассмотрим уравнение для движения авто на одной передаче. Построим в координатах Nv и получим график . Вниз от  отложим , затраченную на преодоление трения в трансмиссии. Если неизвестно, то ее вычисляют: . Затем на график наносим кривую  и , учитывая, что до v=10-15м/с не учитывается, далее f несколько возрастает. Вверх от кривой  отклоняется , т.о. получим  на сопротивление среды. График мощностного баланса для всех передач строится так же, только вместо одной пары кривых  и  будет столько, сколько число передач в КПП. Метод динамической характеристики: Практическое использование методов силового и мощностного баланса затруднительно, т.к. для различных значений φ на график приходится наносить несколько кривых N или , N или w. Кроме этого по силовому и мощностному балансу нельзя сравнивать авто, имеющие различные массы, силовые установки, трансмиссию и т.д., т.к. при движении их в одинаковых условиях P и N, необходимые для преодоления сопротивления дороги, различны. От этих недостатков свободен метод решения уравнений при помощи динамической характеристики, предложенный академиком Е.А. Чудаковым. Динамическая характеристика авто – график зависимости динамического фактора авто с полезной нагрузкой от скорости движения на различных передачах. Для решения уравнения движения сопоставляют величины «Д», рассчитанные по условия тяги и по условию сцепления с коэффициентом сопротивления дороги ψ. Чтобы учесть также ограничения в следствии буксования, определим предельные значения силы тяги по условию сцепления колес с дорогой: . Подставив найденное значение и пренебрегая f, получим выражение динамического фактора по сцепным свойствам: 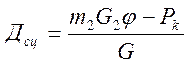. В случае буксования авто скорость невелика.

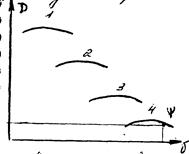Для определения на участке дороги, характеризующимся постоянным коэффициентом ψ надо по оси ординат отложить ψ в том же масштабе, что и Д, и провести прямую, параллельную оси x. АНАЛИЗ: 1.Если линия ψ пересекает кривую Д, то в этой точке , т.к. Д= ψ. 2. Если Д проходит выше ψ, то равномерное движение при открытой дроссельной заслонке невозможно, т.к. происходит разгон авто. Чтобы обеспечить равномерное движение, нужно прикрыть заслонку. 3. Если ψ > Д, то движение с постоянной скоростью невозможно – торможение. Также с помощью динамической характеристики определяется ψ при движении авто с постоянной скоростью. Для этого по динамической характеристике находим величину Д по указанной  скорости следует ψ. Также, если известен f, то определив ψ, можно определить  из выражения: .

Вопрос 8: Расчет ускорения при движении автомобиля. Ускорение во время движения автомобиля определяется на горизонтальной дороге  с твердым покрытием хорошего качестваа при max использовании мощности двигателя и отсутствии буксования ведущих колес. Ускорение (м/с²) находим из выражения 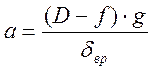,  - коэффициент учета вращающихся масс.   Для определения D помечаем на графике 5..6 значений и  находим соответствующее  значение D и по приведенной формуле  имеем ускорение (a) для заданного коэффициента.  определяется по формуле 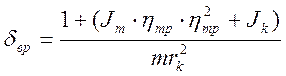,  - момент инерции находится,  - момент инерции колес. На полученные значения a,v строятся графики. Примерное  значение max ускорения автомобиля берем из таблицы.

Вопрос 9: Расчет пути и времени разгона автомобиля. Время равномерного движения автомобиля в реальных условиях невелико по сравнению со временем его работы. При эксплуатации в городе авто двигается равномерно 15-25% времени, 30-45% - ускоренно, 30-40% - движение накатом или торможение. Показателями динамических свойств авто при равномерном движении является ускорение, S и t разгона.