Вопрос 1: Силы, действующие на автомобиль. Основной
движущей силой является сила тяги, приложенная к ведущим колесам. Она возникает
в результате взаимодействия колеса с дорогой. Сила тяги ![]() определяется
как соотношение крутящего момента
определяется
как соотношение крутящего момента ![]() на колесах к радиусу
ведущих колес r:
на колесах к радиусу
ведущих колес r: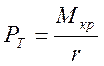 .
. ![]() ;
; ![]() - сила
сопротивления воздуха,
- сила
сопротивления воздуха, ![]() - сила сопротивления подъема,
- сила сопротивления подъема, ![]() -сила инерции
-сила инерции ![]() ,
, ![]() - тяги ,
- тяги , ![]() - сопротивление
качению,
- сопротивление
качению, ![]() - сопротивление дороги. Сила сопротивления
подъему – скатывающая сила
- сопротивление дороги. Сила сопротивления
подъему – скатывающая сила ![]() , на автодорогах с
твердым покрытием уклоны I не
превышают 4-5 °.
, на автодорогах с
твердым покрытием уклоны I не
превышают 4-5 °. ![]() , мощность на преодоление подъема
с уклоном i:
, мощность на преодоление подъема
с уклоном i: ![]() .
Сила сопротивления качению – эта сила зависит от коэффициента деформации дороги
и шины, а также от трения шины о покрытие. Во время качения колеса между
частями шины вследствие их деформации возникает трение и выделяется тепло,
следовательно потери в шинах при качении колеса деформация в передней части
контакта увеличивается, в задней уменьшается.
.
Сила сопротивления качению – эта сила зависит от коэффициента деформации дороги
и шины, а также от трения шины о покрытие. Во время качения колеса между
частями шины вследствие их деформации возникает трение и выделяется тепло,
следовательно потери в шинах при качении колеса деформация в передней части
контакта увеличивается, в задней уменьшается. ![]() . Чем
сильнее колесо , тем труднее его столкнуть. G – составляющая
веса,
. Чем
сильнее колесо , тем труднее его столкнуть. G – составляющая
веса, 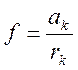 – коэффициент сопротивления качению. При
скоростях 10-15 м/с f=const, но
с увеличением скорости f возрастает,
т.к. шина не успевает полностью в зоне и возвращается не вся энергия,
затраченная на деформацию шины. Кроме того, при увеличении скорости деформации
возникает внутреннее трение в шине. Для движения по хорошим дорогам
– коэффициент сопротивления качению. При
скоростях 10-15 м/с f=const, но
с увеличением скорости f возрастает,
т.к. шина не успевает полностью в зоне и возвращается не вся энергия,
затраченная на деформацию шины. Кроме того, при увеличении скорости деформации
возникает внутреннее трение в шине. Для движения по хорошим дорогам 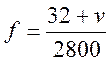 , влияние скорости на величину деформации
, влияние скорости на величину деформации 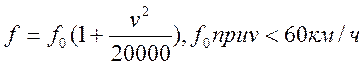
Вопрос 2: Радиусы эластичного колеса. Различают
следующие виды радиусов колеса: 1.Номинальный – радиус подсчитан по номинальным
размерам шин. 2. Свободный (![]() ) – радиус беговой
дорожки при отсутствии всех сил действующих на колесо и при отсутствии его
вращения. 3. Статический (
) – радиус беговой
дорожки при отсутствии всех сил действующих на колесо и при отсутствии его
вращения. 3. Статический (![]() ) – расстояние от оси
колеса до опоры поверхности, при этом колесо нагружено вертикальной силой.
Величина статического радиуса зависит от вертикальной нагрузки и воздуха в
шинах. 4. Динамический (
) – расстояние от оси
колеса до опоры поверхности, при этом колесо нагружено вертикальной силой.
Величина статического радиуса зависит от вертикальной нагрузки и воздуха в
шинах. 4. Динамический (![]() ) – расстояние от оси до
опорной поворота дороги, по которой оно катится. Колесо при этом нагружено
осевой вертикальной и всеми силами. Динамический радиус увеличивается с
уменьшением нагрузки и увеличения давления в шинах. При увеличении скорости под
действием центробежных сил, силы растягиваются в радиальном направлении,
вследствие чего
) – расстояние от оси до
опорной поворота дороги, по которой оно катится. Колесо при этом нагружено
осевой вертикальной и всеми силами. Динамический радиус увеличивается с
уменьшением нагрузки и увеличения давления в шинах. При увеличении скорости под
действием центробежных сил, силы растягиваются в радиальном направлении,
вследствие чего ![]() возрастает. 5. Радиус качения
колеса (
возрастает. 5. Радиус качения
колеса (![]() ) - радиус условного недеформирующегося
катящегося бес скольжения колеса, которое имеет с данным эластичным колесом
одинаковые угловую и линейную скорости. Определяется по формуле:
) - радиус условного недеформирующегося
катящегося бес скольжения колеса, которое имеет с данным эластичным колесом
одинаковые угловую и линейную скорости. Определяется по формуле: 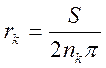 , S – путь,
пройденный колесом, n – число оборотов колеса. Радиус
качения с ростом крутящего момента уменьшается, а с ростом тормозного момента
увеличивается. При полном буксовании
, S – путь,
пройденный колесом, n – число оборотов колеса. Радиус
качения с ростом крутящего момента уменьшается, а с ростом тормозного момента
увеличивается. При полном буксовании ![]() =0, при полном
скольжении
=0, при полном
скольжении ![]() . На дороге с твердым покрытием
. На дороге с твердым покрытием ![]() =
=![]() и измеряется опытным путем.
У радиальных шин легковых автомобилей в обозначении введен индекс в
соответствии h/b, 0,7=H/B.
и измеряется опытным путем.
У радиальных шин легковых автомобилей в обозначении введен индекс в
соответствии h/b, 0,7=H/B.
 Вопрос 3: Коэффициент общего дорожного сопротивления.
Сила сопротивления качению
Вопрос 3: Коэффициент общего дорожного сопротивления.
Сила сопротивления качению ![]() возникает при
деформации шины при взаимодействии с дорогой. При нагружении колеса
вертикальной нагрузкой происходит упругая деформация шины, сопровождающаяся
затратами энергии. При качении колеса по твердой поверхности энергия
затрачивается на трение в материале шины и трение скольжения в контакте шины с
дорогой.
возникает при
деформации шины при взаимодействии с дорогой. При нагружении колеса
вертикальной нагрузкой происходит упругая деформация шины, сопровождающаяся
затратами энергии. При качении колеса по твердой поверхности энергия
затрачивается на трение в материале шины и трение скольжения в контакте шины с
дорогой.
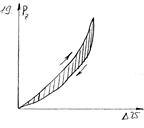
Площадь петли представляет работу, затраченную на потери в шине.
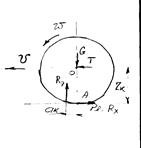 Рассмотрим ведомое колеса. Т – толкающая сила,
Рассмотрим ведомое колеса. Т – толкающая сила, ![]() - реакция от вертикальной нагрузки,
- реакция от вертикальной нагрузки, ![]() - радиус качения колес,
- радиус качения колес, ![]() - сила сопротивления качения. Деформация
в передней части контакта больше, чем в задней части. Реакция
- сила сопротивления качения. Деформация
в передней части контакта больше, чем в задней части. Реакция ![]() на плоскости
на плоскости ![]() создает
момент
создает
момент ![]() . Рассмотрим равновесие колеса для
определенной силы. Т.ч.:
. Рассмотрим равновесие колеса для
определенной силы. Т.ч.: 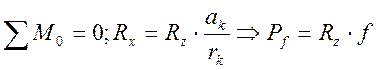 ,
, 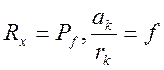 . Коэффициент сопротивления f не изменяется до 90 км/час, а при
более высокой v f увеличивается, т.к. шина в зоне
контакта не успевает полностью распрямиться и колесу возвращается меньшая доля
энергии. При увеличении v создается
внутреннее трение в резине. Влияние v на
деформацию определяется:
. Коэффициент сопротивления f не изменяется до 90 км/час, а при
более высокой v f увеличивается, т.к. шина в зоне
контакта не успевает полностью распрямиться и колесу возвращается меньшая доля
энергии. При увеличении v создается
внутреннее трение в резине. Влияние v на
деформацию определяется: 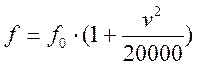 ,
, ![]() - коэффициент (меньше 60 км.)
- коэффициент (меньше 60 км.)
|
Покрытие |
|
f (v > 60 км/час) |
|
Асфальтовое покрытие:
|
0,014 0,018 |
0,018 0,02 |
|
Булыжная мостовая: Гравий Грунт Песок |
0,025 0,02 - - |
0,025-0,03 0,02-0,025 0,03-0,05 0,01-0,03 |
Вопрос 4: Условия возможности движения авто.
Длительное безостановочное движение авто возможно. Тогда у нас ![]() . Это неравенство связывает конструктивные
параметры машины с сопротивлением движения. Условие это необходимое, но не
достаточное, т.к. не учитывается буксование ведущих колес с дорогой. Т.о. с учетом
буксования уравнение примет вид:
. Это неравенство связывает конструктивные
параметры машины с сопротивлением движения. Условие это необходимое, но не
достаточное, т.к. не учитывается буксование ведущих колес с дорогой. Т.о. с учетом
буксования уравнение примет вид: ![]() . Для авто с передними
ведущими колесами в формулу подставляем
. Для авто с передними
ведущими колесами в формулу подставляем ![]() или
или ![]() , задними ведущими колесами
, задними ведущими колесами ![]() или
или ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.