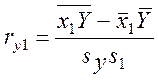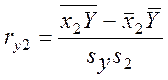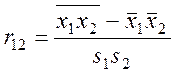Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 28

,   ,   ,

а вибіркові часткові коефіцієнти кореляції за формулами

, , .

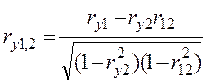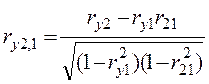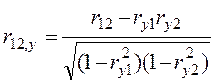Тут s₁, s₂, s_y – вибіркові середні квадратичні відхилення.

Обчислення зазначених тут середніх наведені в розрахунковій табл. 4.2.

Таблиця 4.2

Y	x1	x2			x1x2	x1Y	x2Y	Y2
25,4 26,1 27,8 29,2 30,4 32,4 33,4 35,7 37,4 40	86 82 85 77 81 84 86 88 79 76	230 242 251 262 271 282 294 308 315 331	7396 6724 7225 5929 6561 7056 7396 7744 6241 5776	52900 58564 63001 68644 73441 79524 86436 94864 94225 109561	19780 19844 21335 20174 21951 23688 25284 27104 24885 25156	2184,4 2140,2 2363 2248,4 2462,4 2721,6 2872,4 3141,6 2954,6 3040	5842 6316,2 6977,8 7650,4 8238,4 9136,8 9819,6 10995,6 11781,0 13240,0	645,16 681,21 772,84 852,64 924,16 1049,71 1115,56 1274,49 1398,76 1600,00
317,8	824	2786	68048	786160	229201	26128,6	89997,8	10314,6
31,78	82,4	278,6	6804,8	78616	22920,1	2612,86	8999,78	1031,46

     Далі маємо

,

,

.

,

,

,

,

,

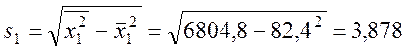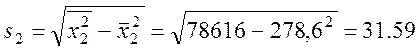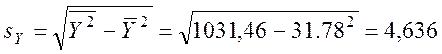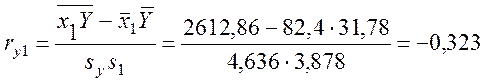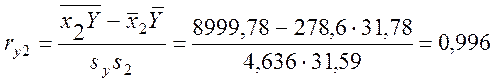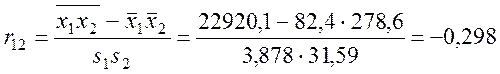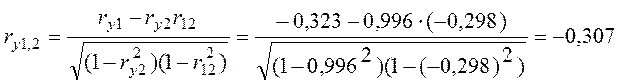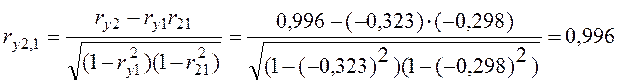Зробимо аналіз отриманих результатів:

а) негативне значення r_y1,2 указує на те, що з ростом витрат прибуток Y буде зменшуватися. Невелике абсолютне значення |r_y1,2| = 0,307 означає слабкий вплив витрат на прибуток;

б) значення вибіркового часткового коефіцієнта кореляції між Y і х₂ (r_y2,1 = 0,996) високе і вказує на тісний зв'язок прибутку і основних фондів;

в) низьке значення r₁₂ = -0,298 означає, що ознаки х₁ і х₂ практично не корелюють. Цей факт дуже важливий у лінійних регресійних моделях.

2  Виберемо в якості функції регресії лінійну

.                                   (4.1)

Система нормальних рівнянь для визначення МНК-оцінок  коефіцієнтів  має вигляд

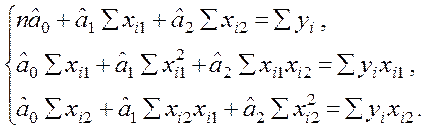     (4.2)

Використовуючи значення зазначених тут сум за даними табл. 4.2, одержуємо

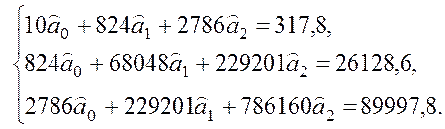
Розв’язуючи вказану систему, отримуємо , , .

Таким чином, оцінене рівняння регресії здобуває вид

.                    (4.3)

Зробимо аналіз регресійної моделі:

а) від’ємне значення коефіцієнта  свідчить про те, що з ростом витрат на 1 грн. зробленої продукції, прибуток підприємства зменшується, причому за інших рівних умов збільшення (зменшення) витрат на 1 коп. веде до зменшення (збільшенню) прибутку в середньому на 34,4 тис. грн. Коефіцієнт еластичності

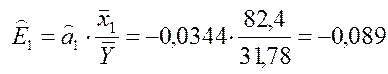
показує, що якщо витрати збільшити (зменшити) на 1%, то прибуток у результаті цього зменшиться (збільшиться) у середньому на 0,089% (за інших рівних умов);

б) позитивне значення коефіцієнта  говорить про те, що з ростом основних фондів прибуток підприємства також росте, причому за інших рівних умов збільшення (зменшення) вартості основних фондів на 1 млн. грн. спричиняє збільшення (зменшення) прибутку в середньому на 144,9 тис. грн. Показник еластичності

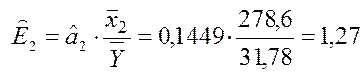
показує, що якщо витрати збільшити (зменшити) на 1%, те це приведе до росту (спаду) прибутку в середньому на 1,27% (за інших рівних умов).

3 Оцінимо тепер якість нашої моделі. Із цією метою обчислимо коефіцієнти детермінації. Маємо

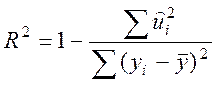=1-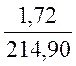 =0,992,

тут  ‑ залишкова сума квадратів, , де  ‑ дані показника Y у вибірці (табл. 4.2),  обчислюється відповідно до формули (4.3). Обчислення дають

, .

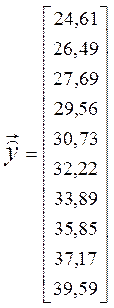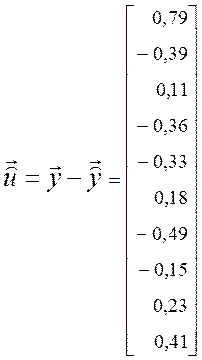Неважко перевірити, що , що свідчить про правильність обчислень.

Значення  свідчить про те, що лінійна модель пояснює 99,2% всієї дисперсії Y, інші 0,8% зв'язані з випадковістю моделі.

Список літератури

1  Назаренко А.М. Эконометрика: Учебное пособие. – Сумы: Изд-во СумГУ, 2000. – 404 с.

2  Назаренко О.М. Основи економетрики: Підручник. - Київ: „Центр навчальної літератури”, 2004. - 392 с.