Відомо, що у випадку нормального розподілу генеральної сукупності Х асиметрія і ексцес дорівнюють нулю, а відповідні вибіркові коефіцієнти асиметрії й ексцесу рівні
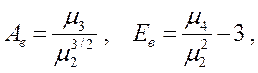 (1.9)
(1.9)
де μk – центральний момент вибірки порядку k, що обчислюється за формулою
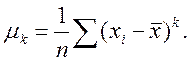 (1.10)
(1.10)
При невеликому об’ємі вибірки Фішер рекомендує в якості оцінок асиметрії А і ексцесу Е розглядати величини
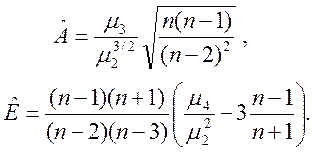 (1.11)
(1.11)
Очевидно, при невеликих значеннях n оцінки ![]() й
й ![]() будуть помітно відрізнятися від вибіркових
Ав й Ев. Виявляється, що у
випадку нормального розподілу оцінки
будуть помітно відрізнятися від вибіркових
Ав й Ев. Виявляється, що у
випадку нормального розподілу оцінки ![]() й
й ![]() мають із великим ступенем точності
нормальні вибіркові розподіли, причому їх математичні сподівання дорівнюють
нулю, а дисперсії визначаються виразами
мають із великим ступенем точності
нормальні вибіркові розподіли, причому їх математичні сподівання дорівнюють
нулю, а дисперсії визначаються виразами
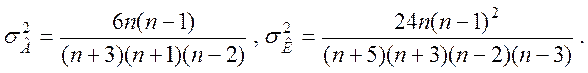 (1.12)
(1.12)
Таким чином, завдання полягає у відповіді на
питання: чи значимо оцінки ![]() і
і ![]() відрізняються від своїх математичних
сподівань, тобто від нуля?
відрізняються від своїх математичних
сподівань, тобто від нуля?
Фішер пропонує користуватися наступним наближеним критерієм згоди:
![]() . (1.13)
. (1.13)
Для обчислення оцінок ![]() і
і
![]() асиметрії А и ексцесу
Е скористаємося даними двох вибірок об’ємів nx
= 10 і ny = 9. Допоміжні обчислення вибіркових
центральних моментів наведені в табл. 1.2 і табл. 1.3.
асиметрії А и ексцесу
Е скористаємося даними двох вибірок об’ємів nx
= 10 і ny = 9. Допоміжні обчислення вибіркових
центральних моментів наведені в табл. 1.2 і табл. 1.3.
Таблиця 1.2 Обчислення центральних моментів першої вибірки
|
xi |
|
|
|
|
|
42 |
1,4 |
1,96 |
2,744 |
3,8416 |
|
43 |
2,4 |
5,76 |
13,824 |
33,1776 |
|
38 |
– 2,6 |
6,76 |
– 17,576 |
45,6976 |
|
40 |
– 0,6 |
0,36 |
– 0,216 |
0,1296 |
|
43 |
2,4 |
5,76 |
13,824 |
33,1776 |
|
38 |
– 2,6 |
6,76 |
– 17,576 |
45,6976 |
|
40 |
– 0,6 |
0,36 |
– 0,216 |
0,1296 |
|
41 |
0,4 |
0,16 |
0,064 |
0,0256 |
|
39 |
– 1,6 |
2,56 |
– 4,096 |
6,5536 |
|
42 |
1,4 |
1,96 |
2,744 |
3,8416 |
|
Σ |
0 |
32,4 |
– 6,48 |
172,272 |
|
Середні |
μ1 = 0 |
μ2 = 3,24 |
μ3 = –0,648 |
μ4 =17,227 |
Таблиця 1.3 Обчислення центральних моментів другої вибірки
|
yj |
|
|
|
|
|
42 |
– 0,333 |
0,111 |
– 0,037 |
0,012 |
|
43 |
0,667 |
0,444 |
0,296 |
0,198 |
|
44 |
1,667 |
2,778 |
4,630 |
7,716 |
|
42 |
– 0,333 |
0,111 |
– 0,037 |
0,012 |
|
44 |
1,667 |
2,778 |
4,630 |
7,716 |
|
43 |
0,667 |
0,444 |
0,296 |
0,198 |
|
40 |
– 2,333 |
5,444 |
– 12,704 |
29,642 |
|
42 |
– 0,333 |
0,111 |
– 0,037 |
0,012 |
|
41 |
– 1,333 |
1,778 |
– 2,370 |
3,160 |
|
Σ |
0 |
14,000 |
– 5,333 |
48,667 |
|
Середні |
μ1 = 0 |
μ2 = 1,556 |
μ3 = –0,593 |
|
Використовуючи дані табл. 1.2, для першої вибірки одержуємо
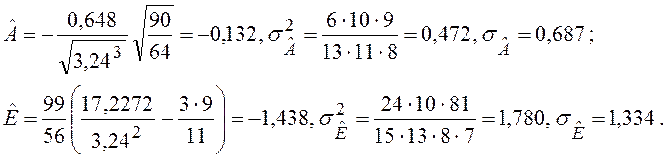
Бачимо, що критерій згоди (1.13) виконується.
Аналогічно за даними табл. 1.3 для другої вибірки знаходимо
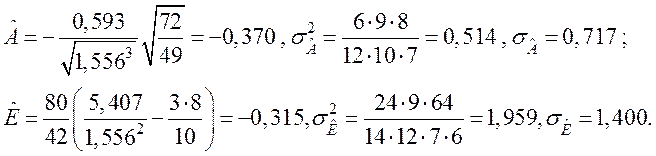
Тут також критерій згоди (1.13) виконується.
Таким чином, дані вибірки погоджуються з нормальним розподілом генеральних сукупностей. Отже, проведені раніше процедури оцінювання математичних сподівань і дисперсій, а також перевірки статистичних гіпотез про рівність математичних сподівань і дисперсій двох генеральних сукупностей виправдані.
Моделювання зростання прибутку фірми
У таблиці 2.1 наведена динаміка росту прибутку фірми за останні 9 років у відсотках до базового (нульовому) року.
Таблиця 2.1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
121,5 |
142,4 |
159,1 |
173,6 |
190,9 |
212,2 |
237,8 |
263,4 |
287,5 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.