Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 21

Приклади розв’язання завдань

Завдання 1

Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму

З метою порівняння кількісних і якісних показників двох однотипних виробничих процесів A і B проведені вибірки (x₁,
x₂, … , x_n) і (y₁, y₂, … , y_n) обсягів n_x і n_y відповідно.

1 Для кожної вибірки оцінити математичне сподівання a і дисперсію σ² шляхом:

а) обчислення вибіркових середніх  і , виправлених вибіркових дисперсій  і ;

б) побудови довірчих інтервалів для математичних сподівань a_x і a_у та дисперсій  і  з надійністю γ = 0,95.

2 Допускаючи, що вибірки (x₁, x₂, … , x_n) і (y₁, y₂, … , y_n) здійснені з нормально розподілених генеральних сукупностей X і Y з параметрами (a_x, ) і (a_y, ) відповідно, при рівні значимості  = 0,05:

а) користуючись критерієм Фішера, перевірити гіпотезу  =  і встановити, чи є один з виробничих процесів ефективнішим іншого;

б) користуючись критерієм Стьюдента, перевірити гіпотезу a_x = a_у і встановити, чи можна вважати розподіл між середніми  і  випадковим, чи він є суттєвим і пов'язаним з відмінністю виробничих процесів.

3 За допомогою критерію згоди Фішера (для малих вибірок) перевірити гіпотези про нормальний розподіл генеральних сукупностей X і Y.

У таблиці 1.1 наведені показники продуктивності праці робітника, який виготовляє на верстаті деталі до (режим роботи A) і після (режим роботи B) удосконалення методу обробки деталей.

Таблиця 1.1 Продуктивності двох різних режимів роботи

Режим роботи	Кількість деталей за зміну
А	42	43	38	40	43	38	40	41	39	42
В	42	43	44	42	44	43	40	42	41

Розв’язання

1 Оцінювання невідомих математичних сподівань і дисперсій

Точечною оцінкою математичного сподівання а генеральної сукупності є вибіркове середнє. Вибіркові середні  і  обчислюються за формулами:

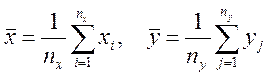                     .                             (1.1)

Часто зручно користуватися формулами

.

У даному випадку маємо

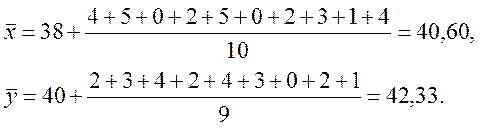
Незсуненою оцінкою дисперсії σ² генеральної сукупності є виправлена вибіркова дисперсія s². Значення  й  будемо обчислювати за формулами:

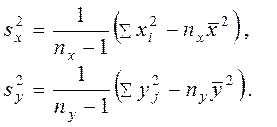                   (1.2)

Оскільки при зменшенні всіх даних вибірки на одне й те саме число значення дисперсії не змінюється, то зменшуючи дані першої вибірки на 38, а другої вибірки на 40, знаходимо

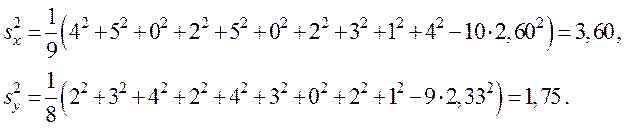
Вибіркове середнє квадратичне відхилення дорівнює квадратному кореню з відповідної вибіркової дисперсії. Тому

Для знаходження довірчого інтервалу математичного сподівання а генеральної сукупності необхідно представити а у вигляді

                                        (1.3)

де  – Точечна оцінка а (середнє вибірки), δ – точність оцінки. Якщо вибірка малого об’єму n, то точність оцінки δ визначається формулою

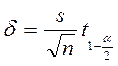.                                      (1.4)

Тут s-вибіркове середнє квадратичне відхилення,  – квантиль розподілу Стьюдента (Додаток А), обчислений при рівні значущості  = 1–γ і k = n–1 ступенях волі.

Для старого режиму роботи А маємо

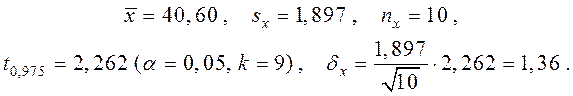
Для нового режиму роботи В

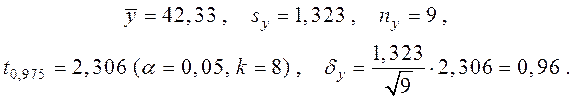 (не 0.96, а 1.0169)

Отже, з надійністю γ = 0,95

,

тобто довірчі інтервали для невідомих математичних сподівань мають вигляд

.

Це означає, що з надійністю 95% при старому режимі обробки деталей робітник міг виготовляти 40 або 41 деталей за зміну. При новому режимі обробки деталей з надійністю 95% він може виготовляти вже 42 або 43 деталей за зміну. Бачимо, що відбулася кількісні зміни в продуктивності праці.

Знайдемо тепер довірчі інтервали для генеральних дисперсій  й . Для дисперсії , генеральної сукупності, довірчий інтервал має вигляд

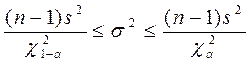                       .                               (1.5)

Тут n – об’єм вибірки, s² – оцінка дисперсії  (виправлена вибіркова дисперсія), і  – квантилі розподілу Пірсона (Додаток Б), обчислені при рівні значущості  і числі ступенів волі k = n–1.

Для старого режиму роботи А