Экономика и менеджмент \ Эконометрика

Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 27

Поліноміальну модель першого порядку шукаємо у вигляді

, де =t-5.

Оцінки  й  параметрів  і  знаходимо по формулах

, .

З огляду на (3.2), маємо 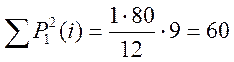. З табл. 3.2 знаходимо 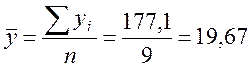,  Тоді

 

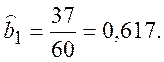
Таким чином, модель першого порядку має вигляд

               (3.11)

Обчислимо дисперсію D1 моделі першого порядку (3.11). Маємо

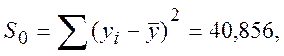
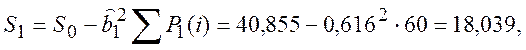
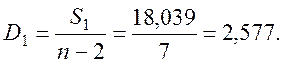
Коефіцієнт детермінації лінійної моделі (3.11)

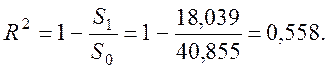
Значення означає, що лінійна модель пояснює 55,8% дисперсії Y, інші 44,2% не обумовлені лінійною моделлю, а зв'язані з випадковістю цієї моделі.

Переходимо до обчислення і оцінки ортогональної регресії другого порядку. У нашому випадку , звідси знаходимо числа , наведені в п'ятому стовпці табл. 3.2. Далі

 ,

 

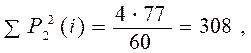
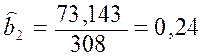З огляду на (3.11) і значення =0,24 знаходимо рівняння моделі другого порядку. Воно має вигляд

.               (3.12)

Тепер

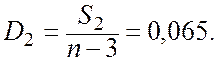
Коефіцієнт детермінації

.

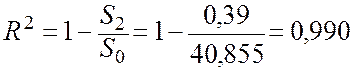Для регресії третього порядку

,  ,

,

                    (3.13)

,  

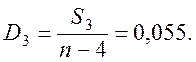
Коефіцієнт детермінації 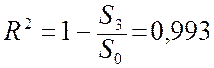 , що незначно перевищує коефіцієнт детермінації моделі другого порядку.

Перевіряємо, чи є рівняння третього порядку значимо кращим у порівнянні з рівнянням другого порядку, чим рівняння другого порядку.

При рівні значимості =0,05 і числі ступенів волі n-4=5 значення tкр =2,571 (Додаток А).

*,  *.

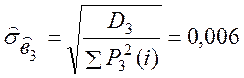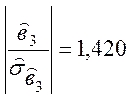Так як 1,420<2,571, то критерій Стьюдента (3.5) не виконується, а тому покладаємо (). До такого ж результату ми прийдемо, використовуючи критерій Фишера (3.7). При рівні значимості  і числах ступенів волі n-3=6 й n-4=5 знаходимо  (Додаток В).

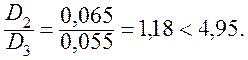
Це означає, що модель третього порядку (3.13) не є значимим поліпшенням моделі другого порядку (3.12).

Зробимо аналіз регресії четвертого порядку

.

Значення  наведені в передостанньому стовпці табл. 3.2, їх можна знайти за рекурентною формулою

,

використовуючи відомі значення P1(i), P2(i) і P3(i). Обчислюємо  і . Маємо

,  ,

, 

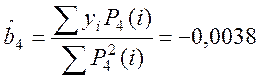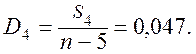
Перевіряємо значимість рівняння четвертого порядку в порівнянні з рівнянням третього порядку. При  і n-5=4 значення  (Додаток А)

,  .

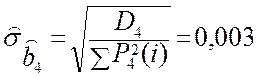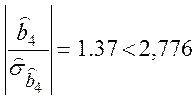Критерій Стьюдента (3.5) значимості  не виконується, тому вважаємо, що .

Аналогічно при рівні значимості  і числах ступенів волі n-3=6 і n-5=4 маємо  (Додаток В)

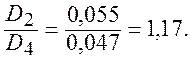
Так як 1,17<6,16, то критерій не виконується, і ми відкидаємо поправку.

Таким чином, аргументи проти b3=0 і b4=0 слабкі, і ми дістаємося висновку, що дані вибірки цілком прийнятно апроксимуються квадратичною моделлю (3.12)

.

Коефіцієнт детермінації, що характеризує якість цієї моделі, .

Зробимо прогноз урожайності зернових на поточний і наступний роки. Маємо

,

.

Завдання 4

Є дані про прибуток (у млн. грн.), витратах на одну грн. зробленої продукції (x1 у коп.) і вартістю основних фондів (x2 у коп.) по даним 10 однотипних підприємств (табл. 4.1).

Таблиця 4.1

Y

25,4

26,1

27,8

29,2

30,4

32,4

33,4

35,7

37,4

40

х1

86

82

85

77

81

84

86

88

79

76

х2

230

242

251

262

271

282

294

308

315

331

Необхідно:

1    Обчислити вибіркові парні коефіцієнти кореляції і вибіркові часткові коефіцієнти кореляції, установити їх значимість при рівні значимості =0,05. Зробити висновки про силу зв'язку показника Y і факторів х1, х2.

2    Методом найменших квадратів оцінити коефіцієнти лінійної регресії  Зробити аналіз оціненої регресії, обчисливши:

а) зміну прибутку при збільшенні величини кожного з факторів на одиницю;

б) середні коефіцієнти еластичності для кожного фактора.

3    Оцінити якість отриманої моделі, обчисливши коефіцієнт детермінації.

Рішення

1 Обчислимо вибіркові парні коефіцієнти кореляції і вибіркові часткові коефіцієнти кореляції за даними табл. 4.1, яка характеризує залежність прибутку від витрат і вартості основних фондів.

Вибіркові парні коефіцієнти кореляції знаходяться за формулами

Скачать файл