Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 22

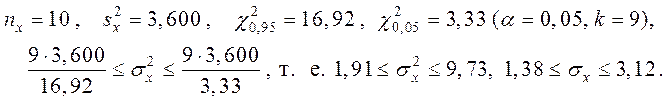
Для нового режиму роботи В

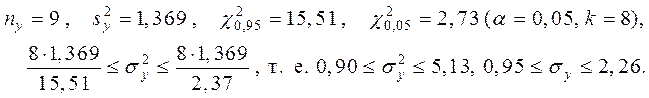
Як бачимо, довірчі інтервали для генеральних дисперсій  і  перетинаються. Тому, з надійністю 95%, у нас немає підстав відхилити гіпотезу про рівність дисперсій (=). Це означає, що вдосконалення обробки деталей не приводить до підвищення ефективності обробки.

2 Перевірка статистичних гіпотез про рівність математичних сподівань і дисперсій

Ефективність виробничого процесу залежить від породжуваної їм дисперсії, що характеризує розкид у даних. Таким чином, для визначення ефективності нового режиму роботи, пов'язаного з удосконаленням обробки деталей, необхідно порівняти генеральні дисперсії  й  по даним вибірок продуктивності праці.

При порівнянні двох дисперсій  і  висувають нульову гіпотезу Н₀:  = , при конкуруючої Н₁:  ≠ . Якщо, за змістом завдання, більшій вибіркової дисперсії () свідомо не може відповідати менша генеральна дисперсія, тобто нерівність < свідомо неможлива, то конкуруюча гіпотеза приймає вигляд Н₁:  > . У цьому випадку для перевірки альтернативної гіпотези Н₁ використовується односторонній критерій Фішера

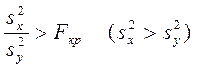                            .                                   (1.6)

Тут F_кр – критичне значення розподілу Фішера (Додаток В), обчислене при рівні значущості  і числі ступенів волі k₁ = n_x–1 і k₂ = n_y–1. Якщо зазначена нерівність виконується, ми схиляємося на корист ь гіпотези Н₁:  > , у противному випадку, у нас немає підстави відхилити нульову гіпотезу
Н₀:  = .

У даному випадку .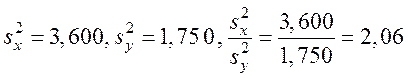
З Додатку В при  = 0,05, k₁ = 9 й k₂ = 8 знаходимо F_кр = 3,39. Так як 2,630 < 3,39, то ми не можемо відхилити нульову гіпотезу і вважаємо рівними генеральні дисперсії  і . Це означає, що вдосконалення обробки деталей, у цьому випадку, не є ефективним.

При порівнянні двох математичних сподівань a_x і a_у висувають нульову гіпотезу Н₀: a_x = a_у, при конкуруючій гіпотезі Н₁: a_x ≠ a_у. Методика перевірки альтернативної гіпотези Н₁ залежить від співвідношення генеральних дисперсій  і .

Раніше при порівнянні двох дисперсій  і  нами було встановлено, що  =  = . У цьому випадку оцінкою дисперсії σ² є середньозважена вибіркова дисперсія

.

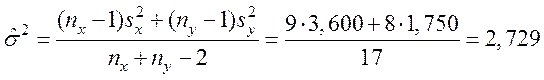Якщо заздалегідь відомо, що більшому вибірковому середньому ( ), не може відповідати менше математичне сподівання (a_у ≥ a_x), то альтернативна гіпотеза приймає вигляд Н₁: a_у > a_x. У цьому випадку для перевірки альтернативної гіпотези Н₁ використається односторонній критерій Стьюдента

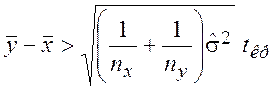                     .                             (1.7)

Тут t_кр – критичне значення розподілу Стьюдента (Додаток А), обчислене при рівні значущості  і числі ступенів волі
k = n_x+n_y–2. Якщо зазначена нерівність виконується, то гіпотеза Н₁ :  a_у > a_x вірна, у противному випадку ми визнаємо правильність нульової гіпотези Н₀ : a_x = a_у.

У цьому випадку =42,33–40,60=1,73. З Додатку А при  = 0,05 й k = 17 знаходимо t_кр = 2,11, тоді

.                 

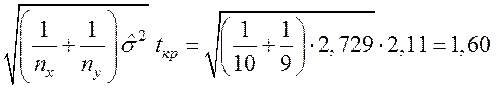Так як 1,60 < 1,73, то ми схиляємося на користь альтернативної гіпотези Н₁ : a_у > a_x. Отже, розбіжність між вибірковими середніми  й  невипадкова, при 5% рівні значущості воно є істотним і приводить до значимого підвищення продуктивності праці після вдосконалення обробки деталей.

Відзначимо, що якщо при порівнянні двох дисперсій  і  було встановлено, що  >  ( ), то для перевірки гіпотези Н₁: a_у > a_x варто використати односторонній критерій Стьюдента вигляду

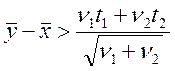                             ,                                     (1.8)

де 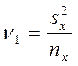, , 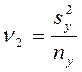t₁ й t₂ – квантилі розподілу Стьюдента (Додаток А), обчислені при рівні значущості  і числах ступенів волі k₁ = n_x–1 й k₂ = n_y–1 відповідно.

3 Перевірка гіпотези про нормальний закон розподілу генеральної сукупності у випадку вибірки малого обсягу

В основі критеріїв згоди, за допомогою яких перевіряється гіпотеза про нормальний розподіл генеральної сукупності лежить порівняння асиметрії і ексцесу нормального закону з їхніми оцінками, отриманими за даними вибірки.