Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 25

Знайдемо середні арифметичне, геометричне і гармонійне для даної вибірки. Маємо

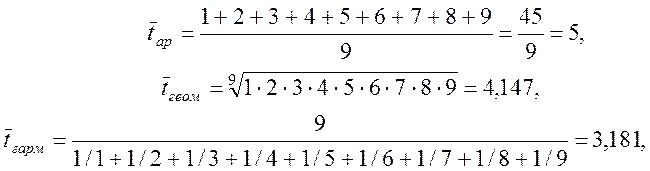
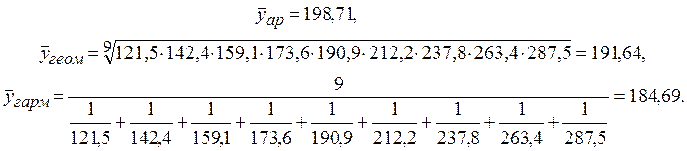
Для вибору оптимальної функції (з дев'яти можливих) порівнюємо , яке відповідає вихідним даним, з отриманим значенням . Якщо  не знаходиться серед вихідних даних, то відповідне значення  можна визначити за допомогою лінійної інтерполяції, провівши через точки (t, Y_t ), (t+1, Y_t+1) пряму. Тут t і t+1 ‑ проміжні значення, між якими знаходиться   З рівняння прямої одержуємо

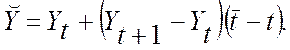.                      (2.5)

В якості критерію вибору найкращої функціональної залежності вибираємо умову мінімуму відносної похибки

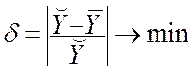.                                (2.6)

У даному випадку

=190,9; ;

Дані розрахунків помістимо в таблицю 2.4.

Таблиця 2.4

№	Вид функції
1		5	198,7	190,9	0,041
2		4,147	198,7	176,14	0,128
3		3,181	198,7	161,72	0,229
4		5	191,64	190,9	0,004
5		4,147	191,64	176,14	0,088
6		3,181	191,64	161,72	0,185
7		5	184,69	190,9	0,032
8		4,147	184,69	176,14	0,049
9		3,181	184,69	161,72	0,142

Аналіз отриманих результатів показує, що найменша відносна похибка  відповідає четвертій функції. Отже, функція  є оптимальною (з дев'яти можливих) і її можна вибрати в якості функції регресії.

4 Якщо вихідна модель характеризується вказаною функцією, то покладаємо  і після логарифмування одержуємо лінійну регресійну модель

 (  .

Відповідно до (2.1), (2.2) для визначення оцінок  і  невідомих параметрів  і  приходимо до системи рівнянь

=>

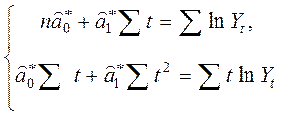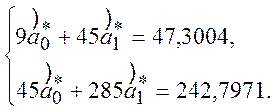
Розв’язуючи отриману систему рівнянь, знаходимо

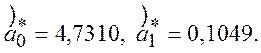
Значення оцінок ,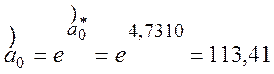

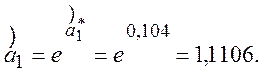
 Шукана показникова функція має вигляд

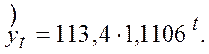
Обчислимо коефіцієнт детермінації отриманої моделі. Для цього будемо користуватися формулою (2.3). Необхідні дані занесемо в табл. 2.5

Таблиця 2.5

t
1	121,5	125,94	-4,44	19,73
2	142,4	139,87	2,53	6,39
3	159,1	155,34	3,76	14,13
4	173,6	172,52	1,08	1,16
5	190,9	191,60	-0,70	0,49
6	212,2	212,79	-0,59	0,35
7	237,8	236,33	1,47	2,16
8+	263,4	262,47	0,93	0,87
9	287,5	291,49	-3,99	15,97
	1788,4	1788,36	0,05	61,25

У цьому випадку , що свідчить про правильність обчислень.

Використовуючи данні табл. 2.5, отримуємо

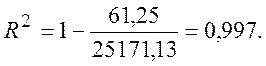
Порівнюючи коефіцієнти детермінації у випадках лінійної та показникової регресій, переконуємося, що показникова функція регресії більш точно описує вихідні данні.

5. Для перевірки обчислимо значення зростання прибутку фірми через 3,5 роки з початку роботи. Для цього підставимо в отримане рівняння, що моделює зростання прибутку фірми, t=3,5. Маємо

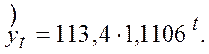
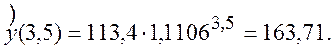
Як і слід було сподіватися, Y₃< < Y₄ (159,1<163,71<173,6).

6 Аналогічним способом зробимо прогноз зростання прибутку фірми на кінець поточні й середину наступних років:

а) у випадку лінійної моделі =96,81+20,38t

б) у випадку показникової моделі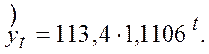

,

.

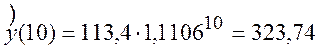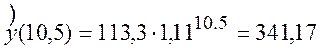Прогнози, обчислені за лінійною і показниковою моделями відрізняються. Однак нами було встановлено, що оптимальною функцією регресії є показникова функція. Тому прогноз, складений за допомогою показникової функції, є більше точним.

Завдання 3

Визначення оптимальної поліноміальної регресії

Нехай для деякого сільгосппідприємства відомі середні врожайності зернових культур за останні 9 років
(табл. 3.1).