Необхідно:
1 Скласти рівняння лінійної регресії. Невідомі коефіцієнти оцінити методом найменших квадратів. Перевірити, що сума відхилень дорівнює нулю. Обчислити коефіцієнт детермінації.
2 Оцінити середній ріст прибутку фірми за рік.
3 Визначити найкращу функцію регресії методом характерних середніх з дев'яти можливих функцій.
4 Для встановленої залежності росту прибутку від номера року методом найменших квадратів визначити оцінки невідомих параметрів. Обчислити коефіцієнт детермінації оптимальної функції регресії.
5 Зробити оцінку величини прибутку через 3,5 роки з початку роботи.
6 За допомогою побудованих лінійної і оптимальної регресії спрогнозувати величину прибутку на кінець поточного і середину наступного років.
1 Рівняння лінійної регресії, що характеризує залежність прибутку Y фірми від часу t шукаємо у вигляді
Y=a0+a1t+u, (2.1)
де а0 і a1 – невідомі коефіцієнти, u – випадковий член, що враховує дію на Y різних факторів (основні фонди, витрати праці і т. п.), помилки в даних, помилки округлень і т. д.
Слідуючи методу найменших квадратів (МНК) для
знаходження оцінок (наближених значень) ![]() і
і ![]() невідомих параметрів а0
і a1 скористаємося системою рівнянь
невідомих параметрів а0
і a1 скористаємося системою рівнянь
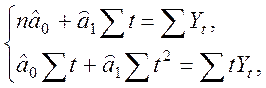 (2.2)
(2.2)
Обчислюємо вказані тут суми. Маємо n=9,
![]() =45,
=45, ![]() =285,
=285, ![]() =10165,
=10165, ![]() =1788,4.
=1788,4.
Тоді вказана система рівнянь приймає вигляд
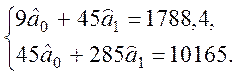
Розв’язуємо отриману систему рівнянь. Для цього помножимо перше рівняння на 5 і віднімемо друге рівняння. Маємо
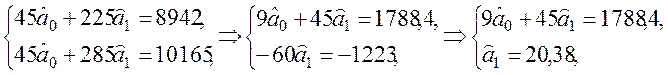
Тепер, підставляючи отримане значення ![]() в
перше рівняння, знаходимо
в
перше рівняння, знаходимо
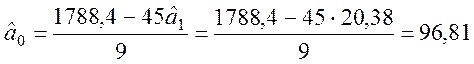 .
.
Таким чином ![]() ,
, ![]() і рівняння шуканої лінійної регресії (2.1)
приймає вигляд
і рівняння шуканої лінійної регресії (2.1)
приймає вигляд
Y=96,81+20,38t+u.
Для перевірки правильності обчислень знайдемо
значення ![]() для
t=1, 2,..., 9 і переконаємося, що
для
t=1, 2,..., 9 і переконаємося, що ![]() =0, де
відхилення
=0, де
відхилення ![]() . Дані обчислень помістимо в табл. 2.2.
. Дані обчислень помістимо в табл. 2.2.
Таблиця 2.2
|
t |
|
|
|
|
|
|
1 |
121,5 |
117,19 |
4,31 |
18,58 |
5961,56 |
|
2 |
142,4 |
137,57 |
4,83 |
23,33 |
3170,94 |
|
3 |
159,1 |
157,95 |
1,15 |
1,32 |
1569,04 |
|
4 |
173,6 |
178,33 |
-4,73 |
22,37 |
630,57 |
|
5 |
190,9 |
198,71 |
-7,81 |
61,00 |
61,01 |
|
6 |
212,2 |
219,09 |
-6,89 |
47,47 |
181,95 |
|
7 |
237,8 |
239,47 |
-1,67 |
2,79 |
1527,94 |
|
8 |
263,4 |
259,85 |
3,55 |
12,60 |
4184,65 |
|
9 |
287,5 |
280,23 |
7,27 |
52,85 |
7883,46 |
|
|
1788,4 |
1788,39 |
0 |
242,31 |
25171,13 |
У цьому випадку ![]() , що
свідчить про правильність обчислень.
, що
свідчить про правильність обчислень.
Коефіцієнт детермінації будемо обчислювати за допомогою формули
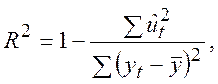 (2.3)
(2.3)
де ![]() ‑ середнє арифметичне елементів вибірки
‑ середнє арифметичне елементів вибірки ![]() .
. ![]() обчислюється
за формулою
обчислюється
за формулою 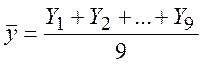 , маємо
, маємо
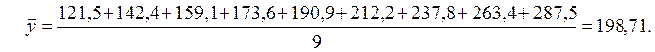
Використовуючи данні табл. 2.2 знаходимо
![]()
![]()
Обчислення коефіцієнту детермінації дають:
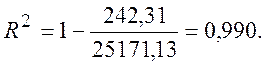
2 Оцінимо середнє ріст прибутку фірми за рік. Вона дорівнює
![]() , (2.4)
, (2.4)
тобто ![]()
3 У цьому випадку прибуток фірми зростає з часом. При моделюванні монотонних процесів може бути використана одна з дев'яти функцій регресії, що залежать від двох параметрів. Вид функції визначається характером середніх (арифметична, геометрична або гармонійна) за часом t і прибутком Yt.
Середнє арифметичне чисел ![]() обчислюється за формулою
обчислюється за формулою
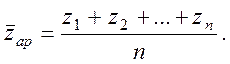
Середнє геометричне додатних чисел ![]() обчислюється за формулою
обчислюється за формулою
![]()
Середнє гармонійне додатних чисел ![]() дорівнює
дорівнює
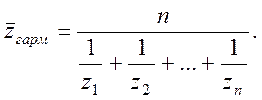
Характерні середні ![]() і
і ![]() для кожної з дев'яти можливих функцій
наведені в табл. 2.3.
для кожної з дев'яти можливих функцій
наведені в табл. 2.3.
Таблиця 2.3
|
№ |
|
|
Вид функції |
Лінеаризована форма |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.